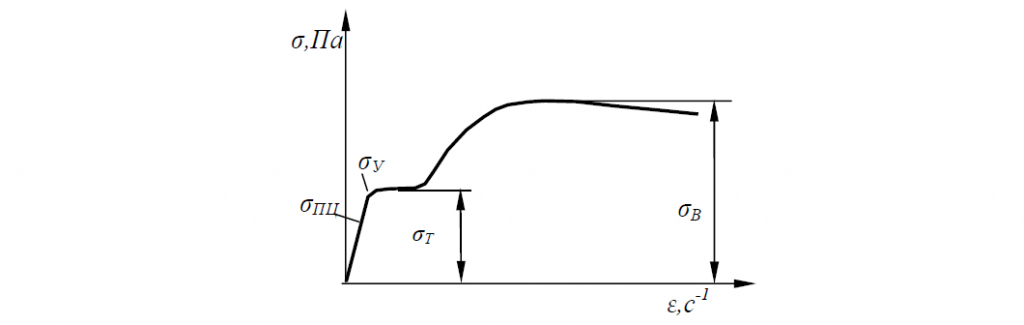
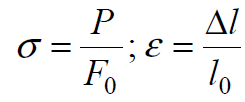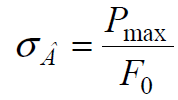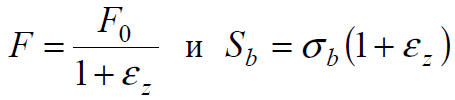Администратор, Автор в Про металлообработку

Фасонные резцы.

Эти резцы применяются для обработки тел вращения, имеющих наружные или внутренние фасонные поверхности. Обработка этими резцами обычно ведется на станках-автоматах и револьверных станках в условиях крупносерийного или массового типа производства. В качестве заготовок деталей чаще всего используют калиброванный прокат в виде прутка.

В сравнении с другими типами резцов фасонные резцы имеют следующие преимущества:

обеспечивают идентичность формы детали и высокую точность размеров, не зависящую от квалификации рабочего;
обладают высокой производительностью за счет большой длины активной части режущей кромки;
имеют большой запас на переточку;
для них достаточно простой переточки по плоскости передней грани;
не требуют больших затрат времени на наладку и настройку станка.

К числу недостатков фасонных резцов можно отнести:

сложность изготовления и высокую стоимость;
это резцы специальные, так как они пригодны для изготовления деталей только заданного профиля;
большие радиальные нагрузки у резцов, работающих с радиальной подачей, вызывают вибрации и упругие деформации нежестких заготовок, что требует снижения подачи и уменьшает производительность;
кинематические передние и задние углы фасонных резцов в процессе резания меняются по длине режущих кромок в большом диапазоне, существенно отличаясь от оптимальных значений.

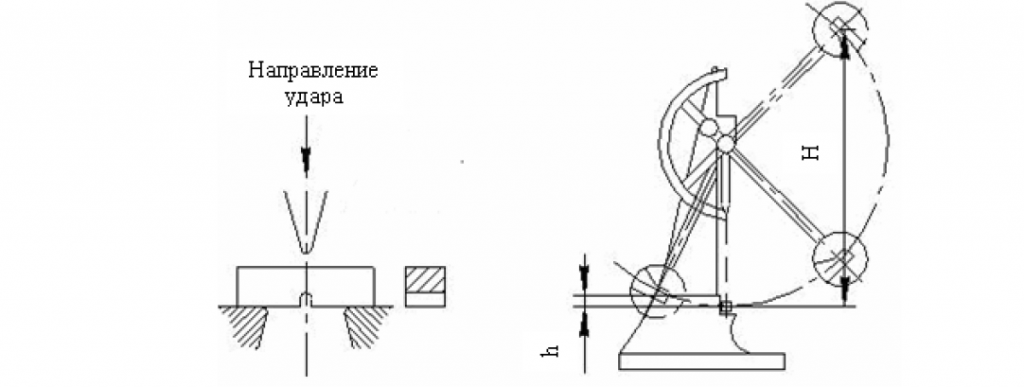
Основные типы фасонных резцов: стержневые (рис. 1, а), круглые (рис. 1, б), призматические радиальные (рис. 1, в), тангенциальные (рис. 1, г). Из них наибольшее применение нашли круглые и призматические резцы, работающие с радиальной подачей.

Стержневые резцы подобны призматическим, но имеют малый запас на переточку. Они применяются в основном для затылования фрез, а также для нарезания резьбы. Крепление этих резцов в суппорте станка подобно креплению токарных резцов.

Призматические тангенциальные резцы позволяют обрабатывать детали малой жесткости, но требуют специальных станков и поэтому на практике применяются очень редко. Их недостатком также является переменность передних и задних углов в процессе снятия припуска.

Сравнение круглых и призматических резцов, работающих с радиальной подачей, показывает, что круглые резцы более технологичны и могут быть изготовлены с большей точностью. Однако они обладают меньшим запасом на переточку и меньшей жесткостью крепления, так как у насадных резцов диаметр оправки зависит от диаметра резца. Последний рекомендуется брать не более 100 мм из-за ухудшения качества быстрорежущей стали, используемой для изготовления таких резцов. Призматические резцы имеют большую жесткость и крепятся с помощью ласточкина хвоста в державках стержневого типа, обладают большим запасом на переточку и, как будет показано ниже, обеспечивают большую точность обработки.

Для обработки внутренних фасонных поверхностей используются только круглые фасонные резцы с креплением на станке с помощью хвостовика, выполненного за одно целое с резцом.

Особенностью фасонных резцов, работающих с радиальной подачей, является переменное значение передних и задних углов по длине режущей кромки.

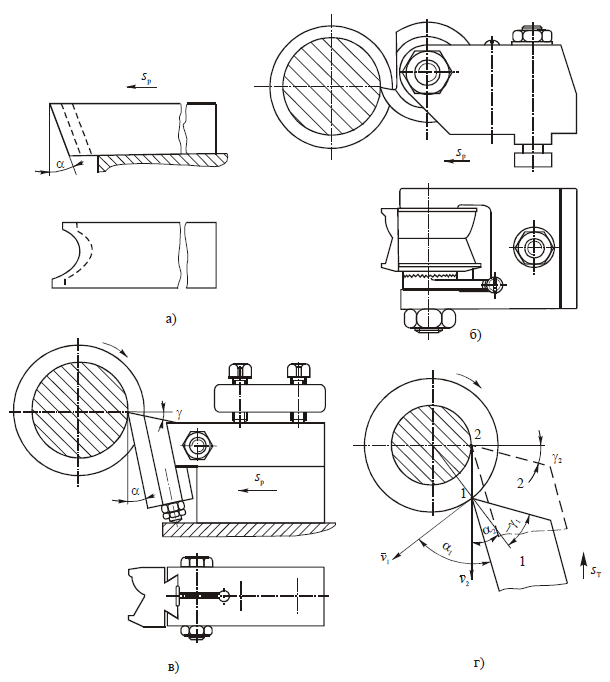
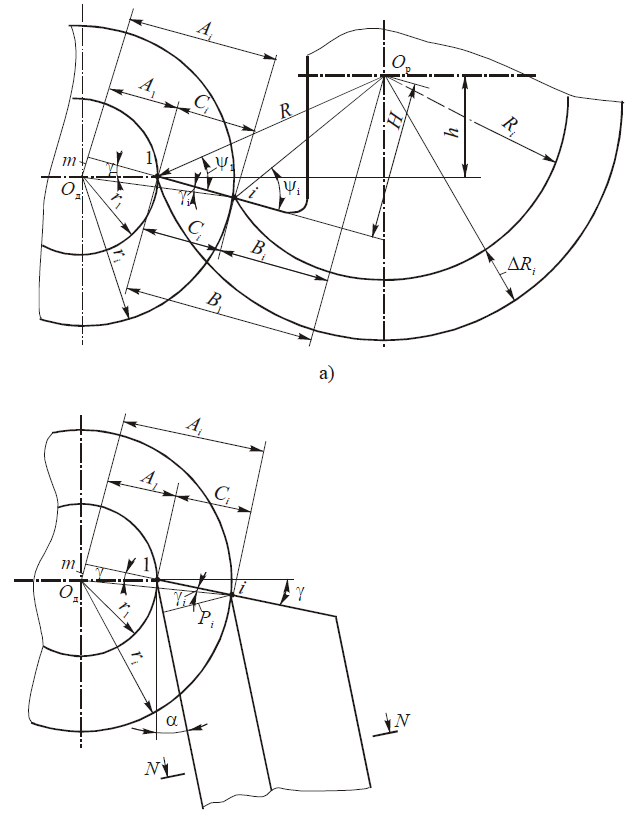
У круглых резцов задний угол α создается за счет превышения центра резца О_р над центром детали О_д на величину h, а передний угол γ — за счет выреза по плоскости передней поверхности, отстоящей от центра на величину H (рис. 2). При этом точки режущей кромки на наружной окружности резца (точки 1 и 3) лежат на линии оси центров станка:

sin а = h / R; sin(α + γ) = sin ψ = H / R,

где R — радиус наружной окружности резца.

Геометрические параметры круглых и призматических фасонных резцов с радиальной подачей — Рис. 2. Геометрические параметры круглых (справа) и призматических (слева) фасонных резцов с радиальной подачей

В других точках режущей кромки углы α и γ в сечении, перпендикулярном к оси резца, зависят от положения координатных плоскостей (основной и резания) и касательных к задней и передней поверхностям. При этом след основной плоскости проходит через режущую кромку и радиус, проведенный в точку режущей кромки из центра детали, а след плоскости резания проходит через вектор окружной скорости резания v. Касательная к задней поверхности в разных точках режущей кромки — это нормаль к радиусу, проведенному из центра резца О_р.

Из сказанного следует, что по мере приближения точки режущей кромки к центру резца происходит поворот координатных плоскостей по часовой стрелке и в любой i-й точке, отстоящей от вершины ближе к центру резца, задний угол α_I > α, а γ_I < γ. Касательные к задней поверхности у круглых резцов также поворачиваются, но в противоположном направлении, т.е. против часовой стрелки. Для расчета переднего угла в любой i-й точке режущей кромки резца опустим перпендикуляр m из центра детали О_д на продолжение передней поверхности резца и найдем, что

m = r₁sin γ = r_i sin γ_i, т.е. sin γ_i = (r_i/r₁)sin γ,

где r_i, r₁ — радиусы точек профиля детали, задаваемые чертежом.

На рис. 2 с левой стороны показано положение призматического резца в процессе резания. При изготовлении этих резцов производится срез по передней грани под углом γ+α, а задний угол α в рабочем положении создается путем поворота резца относительно детали. Приведенные выше формулы, полученные для круглого резца, справедливы и для призматического резца.

Задние углы (a_N) на наклонных режущих кромках принято измерять в сечениях, нормальных к этим кромкам. Во избежание трения задних поверхностей с обработанной поверхностью заготовки они должны быть не менее 1…2°.

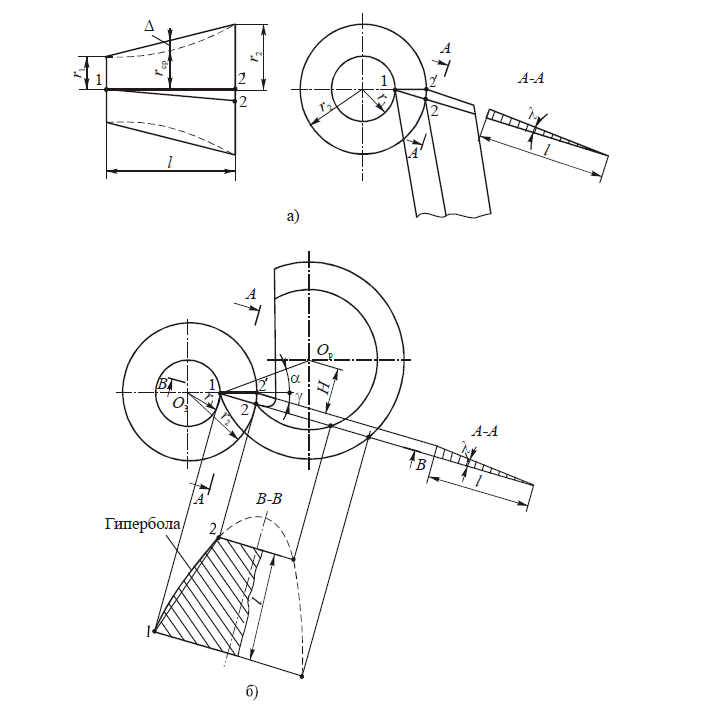
На примере призматического резца (рис. 3, а) с γ = 0 и прямолинейным фасонным профилем найдем, что на участке, параллельном оси детали,

tg α = x / A,

а на наклонном участке режущей кромки в нормальном сечении

tg a_N = y / A

Так как y = x sin φ, где φ — угол между режущей кромкой и нормалью к оси заготовки, то

tg a_N = tg a sin φ.

Из уравнения следует, что при φ → 0 и α → 0 угол a_N → 0 . Во избежание трения боковых задних поверхностей с обработанной поверхностью заготовки участки режущих кромок, перпендикулярные к оси заготовки, выполняют либо с углом поднутрения φ₁=1°30’…3°, либо на них оставляют узкие ленточки шириной f=0,5…1,0 мм (рис. 3, б). При открытых поверхностях возможно изготовление резцов с винтовыми задними поверхностями либо с поворотом оси резца относительно оси заготовки (рис. 3, в). В последнем случае на участке ab, перпендикулярном к оси детали, φ > 0 и, следовательно, a_N > 0.

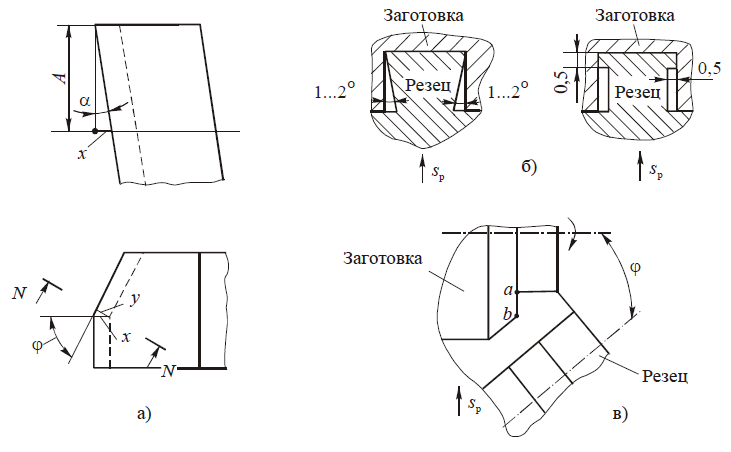
Рис. 3. Задние углы фасонных резцов:
а — задний угол на наклонных режущих кромках; б — поднутрение участков режущих кромок, перпендикулярных к оси заготовки; в — резец с наклонным профилем

Профилирование фасонных резцов (аналитический расчет профиля) необходимо для их изготовления и проектирования инструментов второго порядка, а также шаблонов и контршаблонов, применяемых для контроля соответственно профилей резцов и шаблонов. При этом профиль круглого резца рассчитывается в радиальном (осевом) сечении, а призматического резца — в сечении, нормальном к задней поверхности.

Из-за наличия переменных значений углов a и γ глубина (высота) точек профиля резца в этих сечениях не совпадает с глубиной профиля детали в ее осевом сечении. Расчет ведется путем определения высотных координат характерных (узловых) точек профиля, отсчитываемых от базовой точки, за которую принимается наивысшая точка профиля (вершина резца). Осевые размеры профиля передаются от детали без искажения.

Профилирование круглых фасонных резцов.

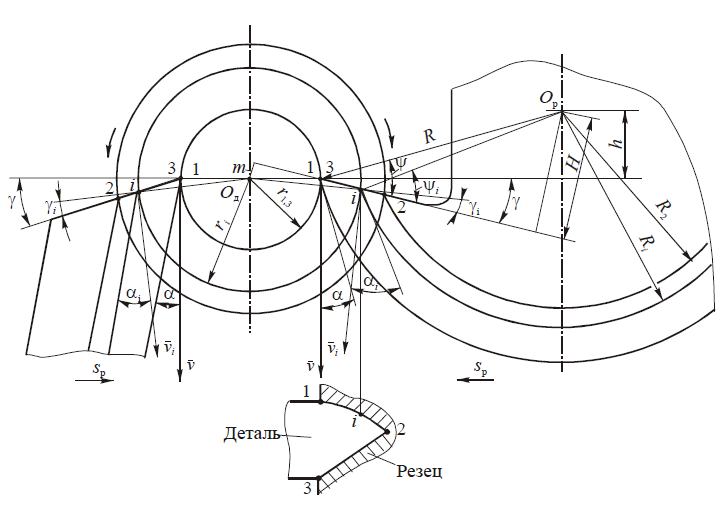
Исходные данные для расчета профиля резца: обрабатываемый материал и профиль детали, задаваемый радиусами окружностей, проходящих через узловые точки r₁, r₂…, r_i, и осевыми размерами a₁, a₂,…, a_i. По рекомендациям выбирают углы вершинной точки γ и a и радиус наружной окружности резца R. Исходя из поставленной задачи, требуется рассчитать радиусы окружностей, на которых лежат точки резца, обрабатывающие соответствующие точки детали R₁, R₂…,R_i и высотные координаты профиля резца в его осевом сечении ΔR = R — R_i (рис. 4, а).

Предварительно определяют параметры вершины резца (точка 1), лежащей на линии центров станка по заданным исходным значениям:

h₁ = R sin a; m = r₁ sinγ; ψ₁ =a + γ; A₁ = r₁ cosγ ; H = Rsin ψ₁; B₁ = R cos ψ₁.

Далее, используя значения этих параметров, для любой i-й точки профиля находят последовательно:

sin γ_i = m / r_i ;

C_i = r_i cos γ_i — A₁ ;

B_i = B₁ -C_i ;

tg ψ_i = H / B_i ;

R_i = H/sin ψ_i ;

ΔR_i = R — R_i.

Здесь параметры A_i, B_i и C_i переменны и измеряются вдоль передней грани резца, а угловой параметр ψ_i = a_i + γ_i определяется с использованием их величин.

Профилирование призматических резцов.

Профилирование призматических резцов производится на основе тех же исходных данных и заключается в определении высотных координат P_i узловых точек профиля резца в сечении, перпендикулярном к задней поверхности инструмента. Из расчетной схемы на рис. 4, б следует, что для этого достаточно иметь три уравнения:

sin γ_i = m/r_i ;

C_i = r_i cos γ_i — A₁ ;

Рис. 4. Расчетные схемы профилирования фасонных резцов:
а – круглый резец; б – призматический резец

Здесь по аналогии с круглыми резцами предварительно находят значения параметров m и А₁. Координаты узловых точек вдоль оси передаются от детали к резцу без искажения.

По найденным координатам узловых точек в указанных сечениях на рабочих чертежах фасонных резцов вычерчивают профиль, обычно в
увеличенном масштабе. При этом прямолинейные участки профиля получают соединением прямой двух крайних точек, а криволинейные — по лекалу через точки отдельных отрезков, на которые предварительно разбивают заданный профиль детали. Обычно берут не менее трех — четырех точек.

Погрешности обработки фасонными резцами.

Погрешности обработки фасонными резцами возникают при обработке конических участков детали из-за несовпадения режущей кромки с образующей конуса.

Рис. 5. Погрешности профиля конических участков заготовок, обработанных фасонными резцами:
а — призматический резец; б — круглый резец

Как следует из рис. 5, а, при обточке усеченного конуса призматическим резцом режущая кромка 1…2 скрещивается в пространстве с осью конуса и при вращении ее относительно оси детали образуется не конус, а однополостной гиперболоид, показанный штриховыми линиями. Наибольшее отклонение фактического профиля от конического Δ приходится на точку профиля с радиусом r_ср = (r + r₂)/2.

Погрешность Δ = r_ср — r_ф, где r_ф — фактический радиус средней точки гиперболоида, который можно найти по формулам аналитической геометрии. При этом величина погрешности Δ не должна превышать допуск на отклонение образующей конуса. В случае применения призматических резцов ее можно свести до нуля, заточив переднюю грань дополнительно под углом λ. При этом режущая кромка резца займет положение 1…2‘, т.е. будет совпадать с образующей конуса.

Из рис. 5, а следует, что

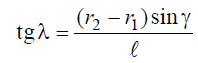
где ℓ — длина конуса.

Такой прием, однако, не дает возможности получить точный конический профиль детали при использовании круглых фасонных резцов. Это объясняется тем, что при пересечении конического тела резца плоскостью передней грани, проходящей параллельно оси, получается криволинейная режущая кромка в форме гиперболы (рис. 5, б). Дополнительная заточка передней грани под углом λ хотя несколько снижает погрешность обработки, но совместить полностью режущую кромку с образующей конуса не удается.

Теоретически можно рассчитать профиль резца по нескольким точкам конической поверхности детали, определив их радиусы в сечениях, перпендикулярных к оси, но тогда профиль исходного тела резца будет криволинейным. Из-за высокой трудоемкости точное изготовление таких резцов считается нерациональным. Заточка же передней грани круглых резцов под углом λ хотя и не исключает погрешности обработки конических участков детали, но дает существенное ее снижение.

Упрочнение и разупрочнение материалов, наклеп и рекристаллизация.

Как следует из диаграмм растяжения, при деформации сталей при комнатной температуре предел текучести увеличивается с ростом деформации, то есть материал в этих условиях упрочняется.

Упрочнение — изменение структуры и свойств металлического материала. вызванное пластической деформацией.

Наибольшую сопротивляемость пластическому деформированию должен оказывать металл с очень малой плотностью дислокаций ρ. По мере увеличения плотности дислокаций ρ сопротивление пластическому деформированию уменьшается (рис. 1).

Рис. 1. Зависимость сопротивления деформированию от плотности дислокаций.

Это происходит до достижения некоторого критического значения плотности дислокаций ρ_кр, когда начинается взаимодействие силовых полей, окружающих дислокации, что и вызывает увеличение сопротивления пластическому деформированию.

Следовательно, увеличение сопротивления пластическому деформированию можно получить двумя путями: наклепом металла, т. е. прямым повышением плотности дислокаций или доведением плотности дислокаций до очень малого значения.

Наклепом называется упрочнение металла при холодной пластической деформации. В результате наклепа прочность (σ_в, σ_0,2, твердость и др.) повышается, а пластичность и ударная вязкость (δ, ψ, KCU) — уменьшаются. Упрочнение возникает вследствие увеличения числа дефектов кристаллической структуры, которые затрудняют движение дислокаций, а следовательно, повышают сопротивление деформации и уменьшают пластичность.

Наклеп является одним из важнейших способов изменения свойств, особенно для сплавов, не упрочняющихся термической обработкой, и для металлов, обладающих пластичностью. Методы упрочняющего воздействия можно разделить на поверхностные (обкатка роликами, дробеструйная обработка) и сквозные (прокатка листов, волочение проволоки). Обработка металлов резанием также приводит к наклепу и изменению структуры в тонком поверхностном слое, что необходимо учитывать при последующей эксплуатации изделий.

Таким образом, пластические деформации вызывают повышение плотности дислокаций, искажение кристаллической решетки и приводят к увеличению напряжения, при котором возможны дальнейшие деформации.

Второй способ — создание металлов и сплавов с бездефектной структурой, — является более прогрессивным. В настоящее время получают кристаллы небольших размеров (длиной 2-10 мм и толщиной 0,5-2,0 мкм), так называемые «усы», практически без дислокаций, с прочностью близкой к теоретической. Такие кристаллы нашли свое применение для армирования волокнистых композиционных материалов, в микроэлектронике и т. д.

Рис. 2. Текстура, возникающая при пластической деформации: а) исходная структура, б) текстура при растяжении, в) текстура при сжатии, г) текстура при сдвиге

При деформировании округлые зерна заменяются вытянутыми в направлении деформации, образуется так называемая текстура (textura — ткань, связь, строение) — анизотропная поликристаллическая пли аморфная среда, состоящая из кристаллов или молекул с преимущественной ориентировкой. Текстуры могут: быть осевыми — с предпочтительной ориентировкой элементов текстуры относительно одного особого направления, плоскими — с ориентировкой относительно особой плоскости и полными — при наличии особой плоскости и особого в ней направления (рис. 2). Текстура создает анизотропию свойств.

Упрочненный металл обладает повышенным запасом внутренней энергии, т. е. находится в неравновесном состоянии. Для приведения металла в равновесное состояние его необходимо нагреть. При нагреве наклепанного металла в нем протекают следующие процессы:

частичное восстановление структурного совершенства в результате уменьшения точечных дефектов за счет увеличения подвижности атомов (избыточные вакансии и межузельные атомы взаимодействуют между собой, а также поглощаются дислокациями при перераспределении последних при нагреве) и снижение внутренних напряжений (процесс возврата):
уменьшение плотности дислокаций за счет аннигиляция противоположных по знаку дислокаций и образование субзерен (полигонов), свободных от линейных несовершенств за счет выстраивания дислокационных стенок (процесс полигонизации):
зарождение и рост новых равноосных зерен вместо ориентированной волокнистой структуры деформированного металла (процесс рекристаллизации).

Процесс рекристаллизации начинается с образования зародышей новых зерен и заканчивается полным замещением деформированного зерна мелкими равноосными зернами (первичная рекристаллизация), в результате чего полностью снимается наклеп, созданный при пластическом деформировании (снижаются прочность и твердость металла и увеличивается его пластичность), металл приобретает равновесную структуру с минимальным количеством дефектов кристаллического строения. Плотность дислокаций после рекристаллизации снижается с 10¹⁰-10¹² см^-2 до 10⁶-10⁸ см^-2.

Рис. 3. Изменение прочности пластичности и зернистого строения в процессе нагрева деформированного металла.

При дальнейшем повышении температуры происходит увеличение размеров наиболее крупных зерен за счет присоединения мелких. С повышением температуры число крупных зерен постепенно растет, пока все мелкие зерна не окажутся присоединенными к крупным — процесс вторичной (собирательной) рекристаллизации.

Температуру начала рекристаллизации, при которой протекает рекристаллизация, происходит разупрочнение холоднодеформированного металла и восстановление его пластичности называют температурным порогом рекристаллизации Т_ПР.

Эта температура не является постоянной физической величиной, как, например, температура плавления. Для данного металла (сплава) она зависит от длительности нагрева, степени предварительной деформации, величины зерна до деформации и т. д. Температурный порог рекристаллизации снижается с повышением степени деформации, увеличении длительности нагрева или уменьшении величины зерна до деформации.

Температура начала рекристаллизации Т_ПР для технически чистых металлов составляет примерно 0,4Т_пл, для чистых металлов снижается до (0,1-0,2)Т_ПЛ, а для сплавов возрастает до (0,5-0,6)Т_ПЛ.

Упругая и пластическая деформация, разрушение.

Любая деформация может осуществляться в твердых телах путем относительного смешения атомов. В твердых телах различают упругую деформацию (исчезающую после устранения воздействия, вызвавшего ее) и пластическую (оставшуюся после удаления нагрузки).

Упругая деформация для твердых тел обычно мала и пропорциональна приложенному напряжению. После снятия нагрузки тело восстанавливает свою форму и размеры. При упругой деформации величина смешения атомов из положения равновесия не превышает расстояния между соседними атомами. При этом величина элементарных сил, вызывающих смешение атомов, возрастает с увеличением этого смешения. Для металлов в определенных пределах нагружения обычно существует пропорциональная зависимость между деформирующими силами (напряжениями) и смешением атомов из положения равновесия (деформациями).

Схема пластической деформации скольжением и двойникованием — Рис. 1. Схема пластической деформации скольжением (а) и двойникованием (б).

С ростом величины упругих деформаций потенциальная энергия твердого тела возрастает. Смешение атомов из положения равновесия является реакцией на действие внешних сил на все твердое тело или его отдельную часть. В любых условиях нагружения действие внешних сил на тело уравновешивается противодействием межатомных, стремящихся вернуть атомы в положение минимума потенциальной энергии.

Однако увеличение потенциальной энергии тела за счет смещения атомов из положения равновесия не может происходить безгранично. При достижении определенного предела потенциальной энергии атомы получают возможность смещаться на расстояния большие, чем межатомные расстояния незагруженного твердого тела. В этом случае после снятия внешних усилий атомы не возвращаются в свои исходные положения равновесия, а занимают новые положения устойчивого равновесия. Сумма смещений атомов в новые положения равновесия создает пластическую деформацию или же остаточное изменение формы и размеров твердого тела в результате действия внешних сил. В этом случае после снятия нагрузки материал не восстанавливает первоначальные форму и размеры.

Для того чтобы смешение атомов в новые положения равновесия не приводило к нарушению сплошности, необходимо, чтобы в процессе такого смешения атомы не удалялись один от другого на расстояния большие, чем размеры зоны активного действия сил взаимного притяжения атомов.

Под нагрузкой атомы всегда смещены из положений равновесия, так как действие внешних сил уравновешивается действием внутренних сил, вызванных смешением атомов из положений равновесия. Отсюда следует, что в условиях пластического деформирования общая (полная) деформация содержит как пластическую составляющую, так и упругую, исчезающую после снятия деформирующих сил.

Так как при снятии деформирующих сил после пластического деформирования атомы стремятся занять положения равновесия (новые) и установить исходные межатомные расстояния, пластическая деформация не может приводить к сколько-нибудь заметному изменению объема деформируемого тела.

Основным механизмом пластической деформации является движение дислокаций (dislocatio — смещение, перемещение). Осуществляется пластическая деформация скольжением и двойникованием (рис. 1. а, б).

Определение твёрдости материалов.

Твердость — способность материала сопротивляться проникновению в него другого, более твердого, материала. Высокой твердостью должны обладать металлорежущие инструменты (резцы, сверла, фрезы и т. д.), а также поверхностно упрочненные детали. Твердость металла определяют способами Бринелля, Роквелла, Виккерса и др. (рис. 1).

Способ Бринелля (ГОСТ 9012-59) основан на том, что в плоскую поверхность металла вдавливают под постоянной нагрузкой закаленный шарик (индентор). Диаметр шарика и величину нагрузки устанавливают в зависимости от твердости и толщины испытуемого металла. Испытание выполняют на приборе ТШ (твердомер шариковый): столик прибора с установленным на нем образцом поднимают до соприкосновения с шариком. Груз опускается и вдавливает шарик в испытуемый образец. На поверхности образца образуется отпечаток. Чем больше диаметр отпечатка, тем металл мягче.

Рис. 1. Схемы определения твердости: а — по Бринеллю; б — по Роквеллу; в — по Виккерсу

За меру твердости НВ принимают отношение нагрузки F к плошали поверхности отпечатка шарика диаметром D:

Диаметр отпечатка измеряют оптической лупой, значение твердости определяют по таблице. Метод прост, достаточно точен и пригоден для измерения твердости материалов до НВ 6500 (средний уровень твердости).

Для испытания твердых материалов применяют способ Роквелла (ГОСТ 9013-59). Способ назван по имени американского металлурга XX века С. П. Роквелла, разработавшего этот метод.

ПО способ Роквелла твердость металлов определяют вдавливанием в испытываемую поверхность алмазного индентора в виде конуса с углом при вершине 120° (шкалы А и С) или стального закаленного шарика диаметром 1/16 дюйма, т. е. 1,588 мм (шкала В). Значение твердости отсчитывают по циферблату индикатора, установленного на приборе.

Твердость по Роквеллу измеряют в условных единицах. За единицу твердости принята величина, соответствующая осевому перемещению наконечника на 0.002 мкм:

При определении твердости способом Виккерса (ГОСТ 2999-75) — от названия английского военно-промышленного концерна «ВИККЕРС» — в поверхность образца вдавливается алмазный индентор (наконечник), имеющий форму правильной четырехгранной пирамиды с двугранным утлом при вершине 136°. При испытаниях применяют нагрузки от 50 до 1000 Н в зависимости от твердости образца.

Числовое значение твердости определяют следующим образом: замеряют с помощью микроскопа длину обеих диагоналей отпечатка после снятия нагрузки и по среднему значению длины диагонали находят в таблице соответствующее значение твердости.

Для измерения твердости металлов в малых объемах (например, в зернах металла) применяют способ определения микротвердости, подобный способу Виккерса.

Для соизмерения значений твердости, определенных различными способами. применяются переводные таблицы (пример: табл. 1).

Для оценки механических свойств материалов и приблизительного значения предела прочности можно использовать значение твердости, определенной по испытаниям способом Бринелля. Эмпирическое соотношение выглядит следующим образом:

σ_в ≈ 0,33HB_max,

где σ_в — временное сопротивление HB_max — максимальное значение твердости при нагрузке, с которой начинается плавное понижение твердости.

Испытание материалов на растяжение и ударную вязкость.

Испытания на растяжение относят к самым распространенным видам механических испытаний, при которых определяется прочность и пластичность материала. Результаты экспериментальных исследований механических свойств материала при одноосном растяжении обычно изображают в виде графиков зависимости напряжения от деформации (рис. 1). Чаше всего испытания проводят при «комнатной» температуре, т. е. при t = 20 °C (или Т = 293 К), и при постоянной и достаточно малой скорости деформации (ε ≈ 1 • 10^-2 n^-1). При этом силу Р, растягивающую образец, относят к первоначальной площади поперечного сечения F_o, а удлинение образца Δl — к первоначальной расчетной длине образца l₀:

т. е. не учитывают изменение площади поперечного сечения образца и предполагают равномерное деформирование образца по его длине.

Условный предел прочности σ_В определяется как отношение максимальной силы Ртах к первоначальной плошали поперечного сечения образца:

Для определения действительного предела прочности S_b максимальную силу Р_тах необходимо относить к действительной площади перечного сечения образца. Поскольку длина образца после деформации dz(1 + ε_z), а площадь поперечного сечения равна F, то согласно постоянству объема до и после деформации: F₀dz=Fdz(1 + ε_z),

откуда

На диаграмме растяжения (см. рис. 1) наблюдаются области упругой деформации, исчезающей после снятия вызвавшей ее нагрузки, и пластической. Между напряжениями и деформациями в области упругости соблюдается закон Гука:

σ_z = Eε_z,

где Е — модуль упругости при растяжении (модуль Юнга).

Модуль упругости Е является константой материала, характеризующей его жесткость. Величина Е выражает сопротивляемость материала упругой деформации при растяжении. Следует отметить, что величина модуля упругости даже для одного и того же материала не является постоянной и колеблется в некоторых пределах. Однако в инженерных расчетах этой разницей можно пренебречь и принять для большинства материалов одно и то же значение Е как при растяжении, так и при сжатии. Модуль упругости является коэффициентом пропорциональности между нормальным напряжением σ и относительной деформацией в и выражается зависимостью:

Е = σ/ε = tg α,

где α — угол наклона прямолинейной части диаграммы растяжения σ = f (ε) к оси абцисс.

Аналогично при сдвиге величина G является коэффициентом пропорциональности между касательным напряжением τ и относительным сдвигом γ и называется модулем упругости при сдвиге или модулем сдвига. Величина G выражается зависимостью:

G = τ/γ.

В связи с тем, что при растяжении или сжатии материал испытывает как продольные ε, так и поперечные ε₁ деформации, их отношение может быть выражено через коэффициент поперечной деформации, называемый также коэффициентом Пуассона μ:

μ = ε₁/ε.

Коэффициент Пуассона так же, как и модули упругости, является характеристикой упругих свойств материала.

Все три константы упругости материала связаны между собой следующей зависимостью:

G = E/2(1 + μ).

Наибольшее напряжение, при снятии которого остаточные деформации не превышают некоторой заданной малой величины (обычно менее 0,2%), называют пределам упругости σ_у.

Если за участком пропорциональности напряжения и деформации следует площадка текучести, соответствующая увеличению деформации при постоянном напряжении (рис. 1), то это напряжение называют пределом текучести σ_т. При отсутствии таковой площадки пределом текучести считают напряжение, соответствующее некоторому установленному небольшому уровню деформации (например, 0,2%) — σ_о,2.

Область справедливости закона Гука устанавливается пределом пропорциональности σ_пц. Поскольку пропорциональность напряжения деформации обычно выполняется во всей области упругости, при практических расчетах предел пропорциональности принимают равным пределу упругости (или меньше).

Для использования диаграмм растяжения при других, более сложных схемах деформирования напряжение σ_z заменяют интенсивностью напряжений σ_i, а деформацию ε_z — интенсивностью деформаций ε_i.

Пластичность характеризуется относительным удлинением и относительным сужением. Относительное удлинение δ это относительное приращение (l_k — l_о) расчетной длины образца после разрыва к его первоначальной расчетной длине l_о, выраженное в процентах:

δ = [(l_k — l_о)/l_о] ⸳ 100%

Относительное сужение ψ — это соотношение разности начальной и конечной плошали (S_o — S_k) поперечного сечения образца после разрыва к начальной площади S_o поперечного сечения, выраженное в процентах:

ψ = [(S_o — S_k)/S_o] ⸳ 100%

Испытания на растяжение не всегда оценивают склонность материала к хрупкому разрушению, поэтому применяют испытания для определения ударной вязкости, отличающиеся от обычных испытаний на растяжение
тем, что образец испытывается на изгиб при ударном (динамическом) нагружении.

Ударная вязкость — способность материала сопротивляться динамическим нагрузкам, определяется как отношение затраченной на излом работы А к площади его поперечного сечения S в месте надреза до испытания: КС = A/S.

Рис. 2. Схема испытания на ударную вязкость: а) образец, б) маятниковый копер

Для испытания (ГОСТ 9454-78) изготавливают стандартные образцы, имеющие форму квадратных брусков с надрезом. Форма надреза может быть округлой. V-образной и в виде трещины. Испытывают образцы на маятниковых копрах. Свободнопадающий маятник копра ударяет по образцу со стороны, противоположной надрезу. При этом фиксируется работа, затраченная на излом образца (рис. 2).

Определение ударной вязкости особенно важно для металлических материалов, работающих при отрицательных температурах и проявляющих склонность к хладноломкости. Чем ниже температура, при которой вязкое разрушение материала переходит в хрупкое, и больше запас его вязкости, тем он надежнее.