Рубрика: Материалы

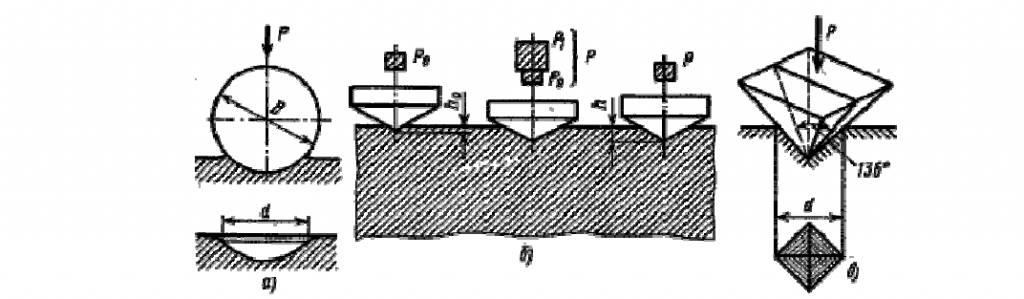
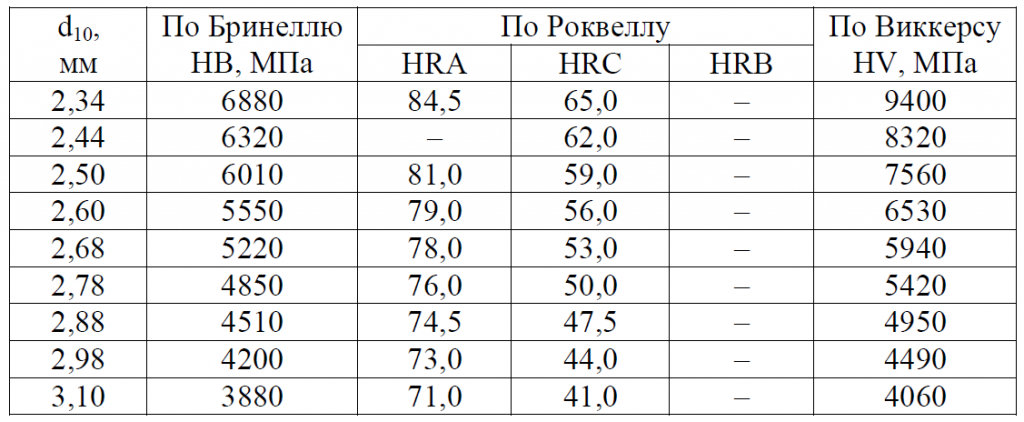
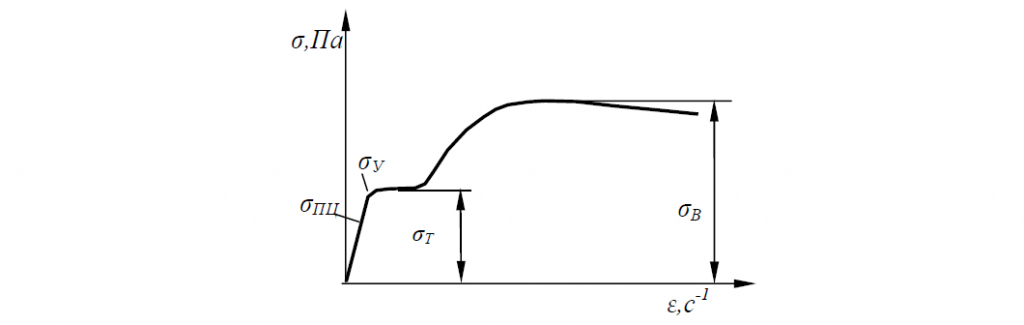
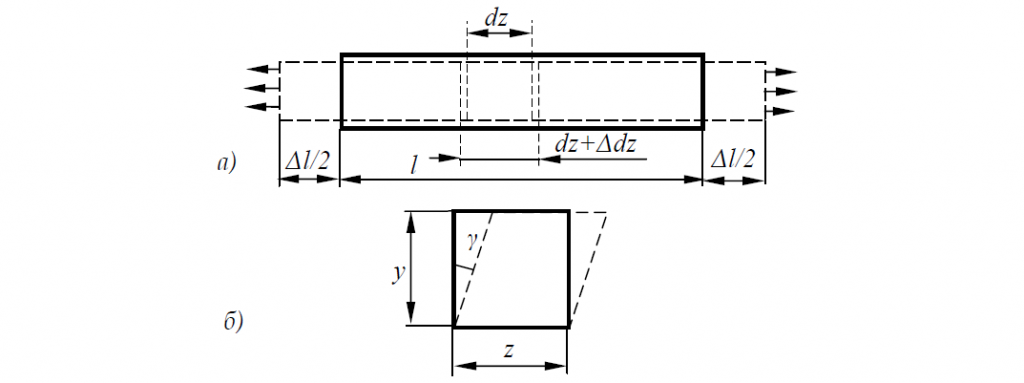
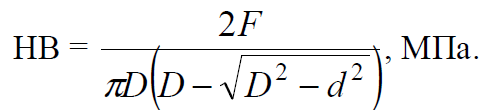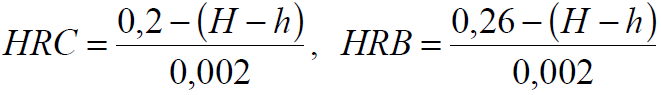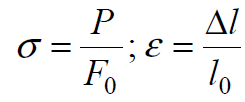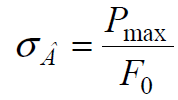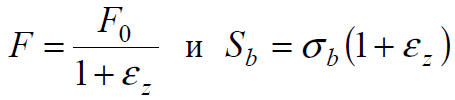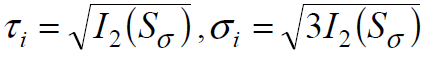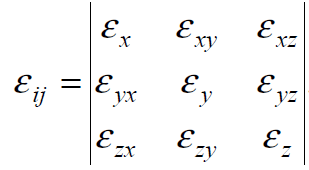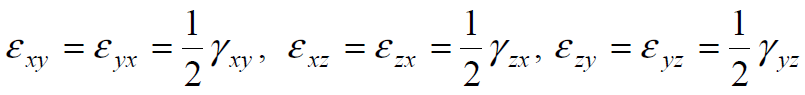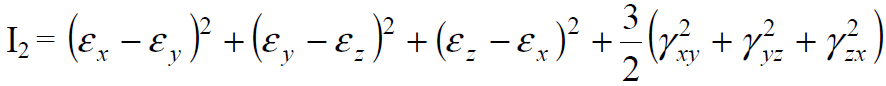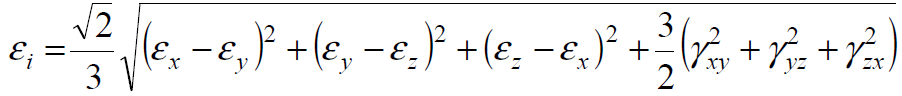Как следует из диаграмм растяжения, при деформации сталей при комнатной температуре предел текучести увеличивается с ростом дефор­мации, то есть материал в этих условиях упрочняется.

Упрочнение — изменение структуры и свойств металлического мате­риала. вызванное пластической деформацией.

Наибольшую сопротивляемость пластическому деформированию должен оказывать металл с очень малой плотностью дислокаций ρ. По ме­ре увеличения плотности дислокаций ρ сопротивление пластическому де­формированию уменьшается (рис. 1).

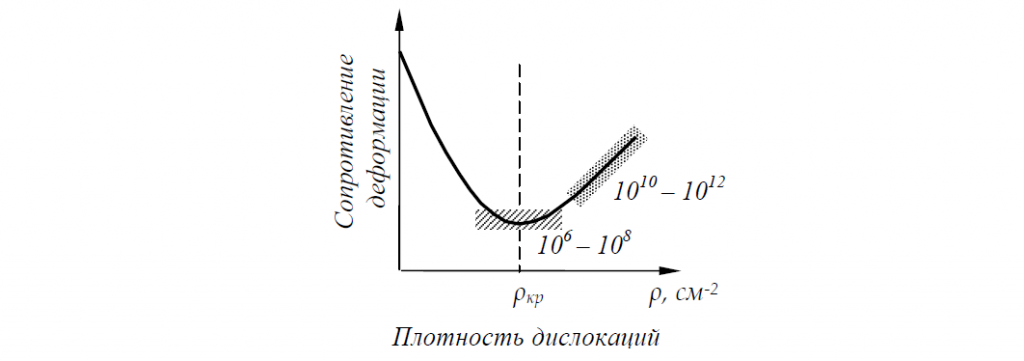
Это происходит до достижения некоторого критического значения плотности дислокаций ρ_кр, когда начинается взаимодействие силовых по­лей, окружающих дислокации, что и вызывает увеличение сопротивления пластическому деформированию.

Следовательно, увеличение сопротивления пластическому деформи­рованию можно получить двумя путями: наклепом металла, т. е. прямым повышением плотности дислокаций или доведением плотности дислока­ций до очень малого значения.

Наклепом называется упрочнение металла при холодной пластической деформации. В результате наклепа прочность (σ_в, σ_0,2, твердость и др.) повышается, а пластичность и ударная вязкость (δ, ψ, KCU) — уменьшаются. Упрочнение возникает вследствие увеличения числа дефектов кристалличе­ской структуры, которые затрудняют движение дислокаций, а следователь­но, повышают сопротивление деформации и уменьшают пластичность.

Наклеп является одним из важнейших способов изменения свойств, особенно для сплавов, не упрочняющихся термической обработкой, и для металлов, обладающих пластичностью. Методы упрочняющего воздейст­вия можно разделить на поверхностные (обкатка роликами, дробеструй­ная обработка) и сквозные (прокатка листов, волочение проволоки). Обра­ботка металлов резанием также приводит к наклепу и изменению структу­ры в тонком поверхностном слое, что необходимо учитывать при после­дующей эксплуатации изделий.

Таким образом, пластические деформации вызывают повышение плот­ности дислокаций, искажение кристаллической решетки и приводят к уве­личению напряжения, при котором возможны дальнейшие деформации.

Второй способ — создание металлов и сплавов с бездефектной структу­рой, — является более прогрессивным. В настоящее время получают кри­сталлы небольших размеров (длиной 2-10 мм и толщиной 0,5-2,0 мкм), так называемые «усы», практически без дислокаций, с прочностью близкой к теоретической. Такие кристаллы нашли свое применение для армирования волокнистых композиционных материалов, в микроэлектронике и т. д.

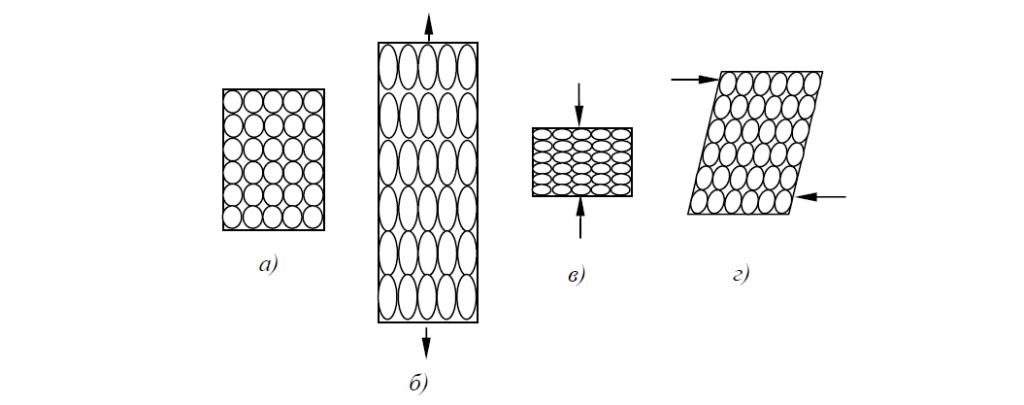
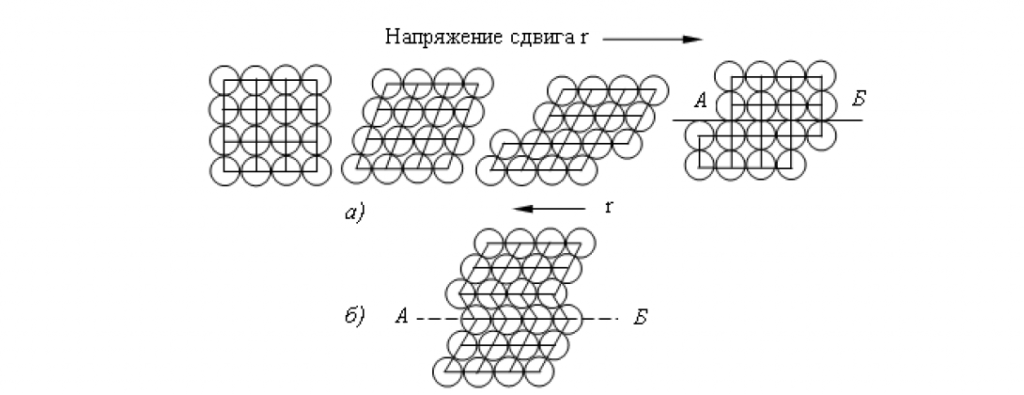
При деформировании округлые зерна заменяются вытянутыми в на­правлении деформации, образуется так называемая текстура (textura — ткань, связь, строение) — анизотропная поликристаллическая пли аморфная среда, состоящая из кристаллов или молекул с преимущественной ориен­тировкой. Текстуры могут: быть осевыми — с предпочтительной ориенти­ровкой элементов текстуры относительно одного особого направления, плоскими — с ориентировкой относительно особой плоскости и полными — при наличии особой плоскости и особого в ней направления (рис. 2). Текстура создает анизотропию свойств.

Упрочненный металл обладает повышенным запасом внутренней энергии, т. е. находится в неравновесном состоянии. Для приведения ме­талла в равновесное состояние его необходимо нагреть. При нагреве на­клепанного металла в нем протекают следующие процессы:

• частичное восстановление структурного совершенства в результате уменьшения точечных дефектов за счет увеличения подвижности атомов (избыточные вакансии и межузельные атомы взаимодействуют между со­бой, а также поглощаются дислокациями при перераспределении послед­них при нагреве) и снижение внутренних напряжений (процесс возврата):
• уменьшение плотности дислокаций за счет аннигиляция противопо­ложных по знаку дислокаций и образование субзерен (полигонов), свобод­ных от линейных несовершенств за счет выстраивания дислокационных стенок (процесс полигонизации):
• зарождение и рост новых равноосных зерен вместо ориентированной волокнистой структуры деформированного металла (процесс рекристалли­зации).

Процесс рекристаллизации начинается с образования зародышей но­вых зерен и заканчивается полным замещением деформированного зерна мелкими равноосными зернами (первичная рекристаллизация), в результа­те чего полностью снимается наклеп, созданный при пластическом дефор­мировании (снижаются прочность и твердость металла и увеличивается его пластичность), металл приобретает равновесную структуру с мини­мальным количеством дефектов кристаллического строения. Плотность дислокаций после рекристаллизации снижается с 10¹⁰-10¹² см^-2 до 10⁶-10⁸ см^-2.

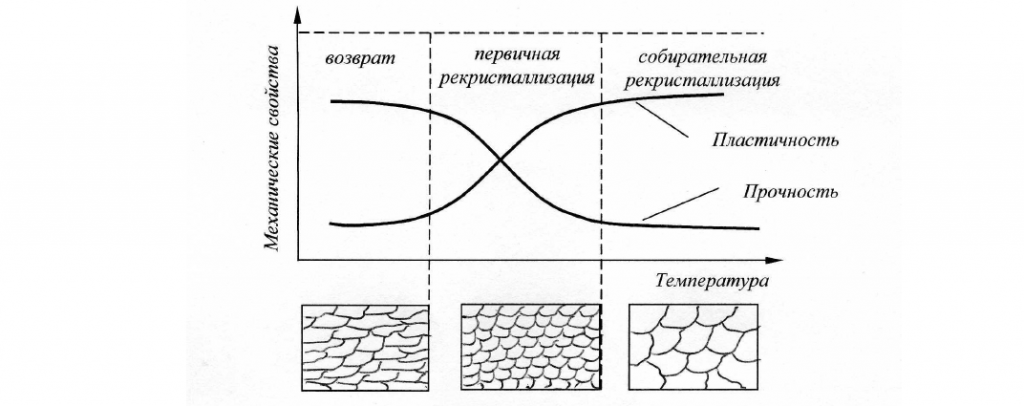
При дальнейшем повышении температуры происходит увеличение размеров наиболее крупных зерен за счет присоединения мелких. С повы­шением температуры число крупных зерен постепенно растет, пока все мелкие зерна не окажутся присоединенными к крупным — процесс вторич­ной (собирательной) рекристаллизации.

Температуру начала рекристаллизации, при которой протекает рекри­сталлизация, происходит разупрочнение холоднодеформированного ме­талла и восстановление его пластичности называют температурным поро­гом рекристаллизации Т_ПР.

Эта температура не является постоянной физической величиной, как, например, температура плавления. Для данного металла (сплава) она зави­сит от длительности нагрева, степени предварительной деформации, вели­чины зерна до деформации и т. д. Температурный порог рекристаллиза­ции снижается с повышением степени деформации, увеличении длитель­ности нагрева или уменьшении величины зерна до деформации.

Температура начала рекристаллизации Т_ПР для технически чистых металлов составляет примерно 0,4Т_пл, для чистых металлов снижается до (0,1-0,2)Т_ПЛ, а для сплавов возрастает до (0,5-0,6)Т_ПЛ.

Любая деформация может осуществляться в твердых телах путем от­носительного смешения атомов. В твердых телах различают упругую де­формацию (исчезающую после устранения воздействия, вызвавшего ее) и пластическую (оставшуюся после удаления нагрузки).

Упругая деформация для твердых тел обычно мала и пропорциональна приложенному напряжению. После снятия нагрузки тело восстанавливает свою форму и размеры. При упругой деформации величина смешения атомов из положения равновесия не превышает расстояния между соседними атомами. При этом величина элементарных сил, вызывающих сме­шение атомов, возрастает с увеличением этого смешения. Для металлов в определенных пределах нагружения обычно существует пропорциональ­ная зависимость между деформирующими силами (напряжениями) и сме­шением атомов из положения равновесия (деформациями).

С ростом величины упругих деформаций потенциальная энергия твер­дого тела возрастает. Смешение атомов из положения равновесия является реакцией на действие внешних сил на все твердое тело или его отдельную часть. В любых условиях нагружения действие внешних сил на тело урав­новешивается противодействием межатомных, стремящихся вернуть ато­мы в положение минимума потенциальной энергии.

Однако увеличение потенциальной энергии тела за счет смещения атомов из положения равновесия не может происходить безгранично. При достижении определенного предела потенциальной энергии атомы полу­чают возможность смещаться на расстояния большие, чем межатомные расстояния незагруженного твердого тела. В этом случае после снятия внешних усилий атомы не возвращаются в свои исходные положения рав­новесия, а занимают новые положения устойчивого равновесия. Сумма смещений атомов в новые положения равновесия создает пластическую деформацию или же остаточное изменение формы и размеров твердого те­ла в результате действия внешних сил. В этом случае после снятия нагруз­ки материал не восстанавливает первоначальные форму и размеры.

Для того чтобы смешение атомов в новые положения равновесия не приводило к нарушению сплошности, необходимо, чтобы в процессе тако­го смешения атомы не удалялись один от другого на расстояния большие, чем размеры зоны активного действия сил взаимного притяжения атомов.

Под нагрузкой атомы всегда смещены из положений равновесия, так как действие внешних сил уравновешивается действием внутренних сил, вызванных смешением атомов из положений равновесия. Отсюда следует, что в условиях пластического деформирования общая (полная) деформа­ция содержит как пластическую составляющую, так и упругую, исчезаю­щую после снятия деформирующих сил.

Так как при снятии деформирующих сил после пластического дефор­мирования атомы стремятся занять положения равновесия (новые) и уста­новить исходные межатомные расстояния, пластическая деформация не может приводить к сколько-нибудь заметному изменению объема дефор­мируемого тела.

Основным механизмом пластической деформации является движение дислокаций (dislocatio — смещение, перемещение). Осуществляется пла­стическая деформация скольжением и двойникованием (рис. 1. а, б).

Испытания на растяжение относят к самым распространенным видам механических испытаний, при которых определяется прочность и пла­стичность материала. Результаты экспериментальных исследований меха­нических свойств материала при одноосном растяжении обычно изобра­жают в виде графиков зависимости напряжения от деформации (рис. 1). Чаше всего испытания проводят при «комнатной» температуре, т. е. при t = 20 °C (или Т = 293 К), и при постоянной и достаточно малой скорости деформации (ε ≈ 1 • 10^-2 n^-1). При этом силу Р, растягивающую образец, относят к первоначальной площади поперечного сечения F_o, а удлинение образца Δl — к первоначальной расчетной длине образца l₀:

т. е. не учитывают изменение площади поперечного сечения образца и предполагают равномерное деформирование образца по его длине.

Условный предел прочности σ_В определяется как отношение макси­мальной силы Ртах к первоначальной плошали поперечного сечения образца:

Для определения действительного предела прочности S_b максималь­ную силу Р_тах необходимо относить к действительной площади перечного сечения образца. Поскольку длина образца после деформации dz(1 + ε_z), а площадь поперечного сечения равна F, то согласно постоянству объема до и после деформации: F₀dz=Fdz(1 + ε_z),

откуда

На диаграмме растяжения (см. рис. 1) наблюдаются области упру­гой деформации, исчезающей после снятия вызвавшей ее нагрузки, и пла­стической. Между напряжениями и деформациями в области упругости соблюдается закон Гука:

σ_z = Eε_z,

где Е — модуль упругости при растяжении (модуль Юнга).

Модуль упругости Е является константой материала, характеризую­щей его жесткость. Величина Е выражает сопротивляемость материала уп­ругой деформации при растяжении. Следует отметить, что величина моду­ля упругости даже для одного и того же материала не является постоянной и колеблется в некоторых пределах. Однако в инженерных расчетах этой разницей можно пренебречь и принять для большинства материалов одно и то же значение Е как при растяжении, так и при сжатии. Модуль упруго­сти является коэффициентом пропорциональности между нормальным на­пряжением σ и относительной деформацией в и выражается зависимостью:

Е = σ/ε = tg α,

где α — угол наклона прямолинейной части диаграммы растяжения σ = f (ε) к оси абцисс.

Аналогично при сдвиге величина G является коэффициентом пропор­циональности между касательным напряжением τ и относительным сдви­гом γ и называется модулем упругости при сдвиге или модулем сдвига. Ве­личина G выражается зависимостью:

G = τ/γ.

В связи с тем, что при растяжении или сжатии материал испытывает как продольные ε, так и поперечные ε₁ деформации, их отношение может быть выражено через коэффициент поперечной деформации, называемый также коэффициентом Пуассона μ:

μ = ε₁/ε.

Коэффициент Пуассона так же, как и модули упругости, является ха­рактеристикой упругих свойств материала.

Все три константы упругости материала связаны между собой сле­дующей зависимостью:

G = E/2(1 + μ).

Наибольшее напряжение, при снятии которого остаточные деформа­ции не превышают некоторой заданной малой величины (обычно менее 0,2%), называют пределам упругости σ_у.

Если за участком пропорциональности напряжения и деформации следует площадка текучести, соответствующая увеличению деформации при постоянном напряжении (рис. 1), то это напряжение называют пре­делом текучести σ_т. При отсутствии таковой площадки пределом текуче­сти считают напряжение, соответствующее некоторому установленному небольшому уровню деформации (например, 0,2%) — σ_о,2.

Область справедливости закона Гука устанавливается пределом пропорциональности σ_пц. Поскольку пропорциональность напряжения деформации обычно выполняется во всей области упругости, при практиче­ских расчетах предел пропорциональности принимают равным пределу упругости (или меньше).

Для использования диаграмм растяжения при других, более сложных схемах деформирования напряжение σ_z заменяют интенсивностью на­пряжений σ_i, а деформацию ε_z — интенсивностью деформаций ε_i.

Пластичность характеризуется относительным удлинением и относи­тельным сужением. Относительное удлинение δ это относительное при­ращение (l_k — l_о) расчетной длины образца после разрыва к его первона­чальной расчетной длине l_о, выраженное в процентах:

δ = [(l_k — l_о)/l_о] ⸳ 100%

Относительное сужение ψ — это соотношение разности начальной и конечной плошали (S_o — S_k) поперечного сечения образца после разрыва к начальной площади S_o поперечного сечения, выраженное в процентах:

ψ = [(S_o — S_k)/S_o] ⸳ 100%

Испытания на растяжение не всегда оценивают склонность материала к хрупкому разрушению, поэтому применяют испытания для определения ударной вязкости, отличающиеся от обычных испытаний на растяжение
тем, что образец испытывается на изгиб при ударном (динамическом) на­гружении.

Ударная вязкость — способность материала сопротивляться динамиче­ским нагрузкам, определяется как отношение затраченной на излом рабо­ты А к площади его поперечного сечения S в месте надреза до испытания: КС = A/S.

Для испытания (ГОСТ 9454-78) изготавливают стандартные образцы, имеющие форму квадратных брусков с надрезом. Форма надреза может быть округлой. V-образной и в виде трещины. Испытывают образцы на ма­ятниковых копрах. Свободнопадающий маятник копра ударяет по образцу со стороны, противоположной надрезу. При этом фиксируется работа, за­траченная на излом образца (рис. 2).

Определение ударной вязкости особенно важно для металлических материалов, работающих при отрицательных температурах и проявляю­щих склонность к хладноломкости. Чем ниже температура, при которой вязкое разрушение материала переходит в хрупкое, и больше запас его вязкости, тем он надежнее.

Напряжение — мера внутренних сил, возникающих в материале под влиянием внешних воздействий (нагрузок, изменения температуры и пр.). Для изучения напряжений через произвольную точку тела мысленно про­водится сечение (рис. 1) и отбрасывается одна из половин тела. Дейст­вие отброшенной половины на другую половину заменяют внутренними силами.

В малом элементе сечения площадью dS в окрестности произвольной точки А действует произвольно направленная внутренняя сила dF. Отношение р = dF/dS называется вектором напряжения в точке А по площадке dS. Составляющие вектора напряжения, действующие по норма­ли к площадке, обозначаются σ и называются нормальными напряжения­ми, а действующие вдоль площадки называются касательными напряже­ниями τ в точке А по площадке dS, причём σ²+τ²=р².

В общем случае напряженное состояние тела в точке А характеризует­ся совокупностью всех векторов напряжений для всевозможных сечений (площадок, проходящих через точку А), а значит и для любого направле­ния. Напряженное состояние в точке А может быть определено с помощью тензора напряжений и характеризуется девятью компонентами по трем сям координат (три нормальных и шесть касательных). Касательные на­пряжения попарно равны (τ_xy = τ_yx, τ_xz = τ_zx, τ_yz = τ_zy,), т. е. остается всего шесть компонентов. Напряжения выражаются в Па (паскалях).

Для тензора характерным является закон, по которому преобразуется его компоненты при повороте осей координат. При повороте системы ко­ординат можно отыскать такое ее положение, когда касательные напряже­ния будут равны нулю. Эти направления называют главными.

Главные направления тензора напряжений определяются условием, зависящим от трех инвариантов I₁, I₂, I₃.

Первым инвариантом I₁ тензора напряжений является сумма нор­мальных напряжений:

I₁ ⁼ σ_x + σ_y + σ_z = Зσ₀

Среднее значение трёх нормальных напряжений называют гидроста­тическим давлением:

σ₀ = (σ_x + σ_y + σ_z)/3

Гидростатическому давлению соответствует тензор напряжений, нор­мальные компоненты которого равны σ₀, а касательные — нулю. Поскольку гидростатическое давление не вызывает в металле пластических деформа­ций, его исключают из системы напряжений. Оставшуюся часть тензора называют девиатором напряжений S_σ:

Второй инвариант I₂ тензора напряжений определяется следующим выражением:

I₂=σ_x σ_y + σ_x σ_z + σ_y σ_z — τ²_xy — τ²_yz — τ²_zx

Величины, пропорциональные корню квадратном из второго инвари­анта девиатора напряжений, называют интенсивностью касательных напряжений τ_i и интенсивностью нормальных напряжений σ_i:

Напряжения в материале могут возникнуть при физико-химических процессах, при неравномерном распределении температуры (при нагреве и охлаждении металла), а также вследствие фазовых превращений при тер­мической обработке. При этом напряжения, возникающие в объеме всего тела, называют макронапряжениями (или напряжениями I рода), а напряжения, возникающие в объеме одного зерна, называют микронапряже­ниями (или напряжениями II рода). Напряжения, возникающие в объемах порядка нескольких параметров кристаллической решетки, называются субмикроскопическими (или напряжениями III рода). Деформациями назы­вают изменения формы или размеров тела (или части тела) под действием внешних сил, а также при нагревании или охлаждении и других воздейст­виях, вызывающих изменение относительного положения частиц тела (рис. 2).

С геометрической точки зрения деформированное состояние в точке описывается тензором деформации:

Компоненты ε_x, ε_y, ε_z характеризуют линейные деформации воло­кон, расположенных по осям х, у, z: относительные удлинения (или отно­сительные укорочения), а компоненты ε_xy, ε_xz, ε_yz— углы поворота двух взаимно перпендикулярных до деформации волокон (или деформации сдвига).

Для компонент деформаций сдвига справедливы равенства:

При повороте системы координат все компоненты тензора деформа­ции преобразуются по определенным линейным относительно направ­ляющих косинусов соотношениям. В теории деформации и линейных пре­образований доказывается, что из всех возможных направлений осей ко­ординат существует тройка взаимно перпендикулярных направлений (главных направлений), относительно которых все сдвиговые компоненты деформации равны нулю. Главные направления деформаций определяются тремя скалярными величинами, не зависящими от положения системы ко­ординат и поэтому называемыми инвариантами.

Первый инвариант I₁ = ε_x + ε_y + ε_z используется для записи условия по­стоянства объема деформируемого металла:

I₁ = ε_x + ε_y + ε_z = 0

Второй инвариант тензора деформации имеет вид:

Величина, пропорциональная корню квадратному из второго инвари­анта называется интенсивностью деформаций и используется для характеристики деформаций в общем случае деформированного состояния.

Простейшие схемы деформирования — растяжение, сжатие, сдвиг, кручение, изгиб. Первые две схемы (растяжение и сжатие) могут быть описаны только линейными компонентами, вторые (сдвиг, кручение, из­гиб) — только сдвиговыми (угловыми).