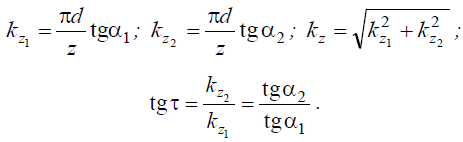Эти фрезы получили широкое распространение в машиностроении, главным образом при обработке деталей с фасонными профилями. Некоторые из фрез стандартизованы: полукруглые, пазовые, дисковые, червячные (для нарезания зубчатых колес), гребенчатые (для нарезания резьбы) и др. Их изготавливают чаще всего в виде насадных фрез — дисковых или цилиндрических, реже — концевых фрез с фасонными главными режущими кромками. В процессе эксплуатации такие фрезы перетачиваются только по передней грани.
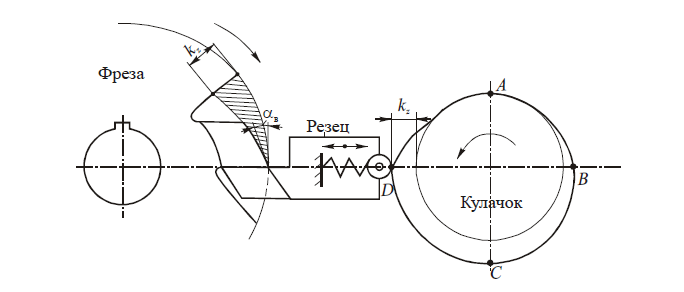
Для создания задних углов на фасонных режущих кромках фрезы используется процесс затылования, осуществляемый на специальных станках по схеме (рис. 1). Здесь фреза вращается вокруг оси, а затыловочный резец с фасонной режущей кромкой совершает возвратно-поступательные движения. Резец приближается к центру фрезы при ее повороте на 1/z оборота, а затем отскоком отходит от фрезы после обработки одного зуба и при подходе следующего. Цикл этих движений повторяется на каждом зубе, т.е. за один оборот фрезы резец совершает z возвратно-поступательных движений. Чтобы полностью обработать заднюю поверхность зубьев, фреза в процессе затылования делает несколько оборотов, так как за один оборот резец не может обработать большую площадь задней поверхности зуба, которая в конечном итоге представляет собой совокупность бесконечного числа следов фасонных режущих кромок резца, расположенных в радиальном сечении и сдвинутых одно относительно другого в направлении к центру фрезы. Благодаря этому создаются задние углы во всех точках режущих кромок, а при переточке по передней грани их форма в радиальном сечении будет оставаться неизменной.
При затыловании каждая точка режущих кромок перемещается по кривой затылования с приближением к центру фрезы по мере ее поворота. При этом, чтобы задние углы имели положительное значение, траектория движения каждой точки должна быть расположена внутри окружности, проведенной через эту точку из центра фрезы.
Форма кривой затылования задается формой кулачка (см. рис. 1), который управляет перемещением резца по мере поворота фрезы. При этом участок кулачка ABCD определяет рабочий ход затыловочного резца, а участок DA — холостой ход, при котором резец отходит от зуба фрезы. Полученная кривая затылования определяет картину изменения задних углов в процессе переточки и их величину в различных точках режущей кромки по высоте зуба.
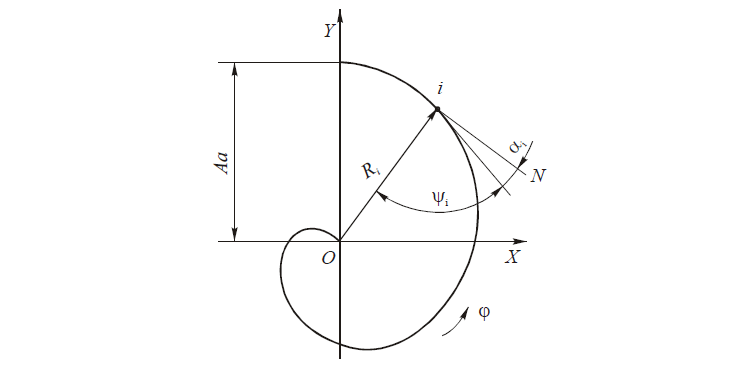
К форме кривой предъявляются следующие требования: 1) задние углы при переточках и при изменении расстояния точки по высоте зуба не должны уменьшаться; 2) форма кулачка должна быть простой в изготовлении и не зависеть от диаметра фрезы и числа зубьев. Из известных кривых, применявшихся для затылования (логарифмическая и архимедова спирали, конхоида прямой и др.), этим требованиям лучше всего отвечает архимедова спираль (рис. 2), которая и нашла наибольшее применение на практике. Она образуется от центра, и при повороте радиуса-вектора вокруг оси его величина увеличивается пропорционально углу поворота. Отсюда уравнение архимедовой спирали в полярных координатах имеет вид
Ri = αφi
где Ri — значение радиуса-вектора при его повороте на угол φi; α — коэффициент пропорциональности.
Профиль кулачка по архимедовой спирали можно весьма просто получить на любом токарном станке при поперечной подаче резца, которая кинематически согласована с вращением шпинделя станка.
Уравнение можно записать также в виде
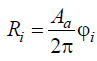
где Aα — характеристика (шаг) архимедовой спирали (при повороте радиуса-вектора на один оборот вокруг центра, т.е. на угол φi = 2π, величина Ri = Aα).
Для любой i-й точки кривой затылования найдем задний угол αi, как угол между нормалью N к радиусу-вектору Ri и касательной к этой кривой. Дополнением до 90° к нему будет угол ψi, т.е. αi+ψi = 90°. Из аналитической геометрии известно, что tgψi, равен отношению функции Ri = αφi к ее производной, т.е.
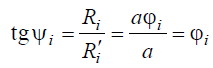
следовательно,
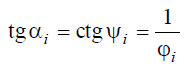
Используя уравнение Ri = αφi, можно выразить αi как
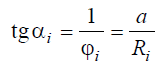
Из этого уравнения следует, что по мере переточки зуба фрезы радиус-вектор Ri будет уменьшаться и, следовательно, будет увеличиваться и задний угол αi. В точках, лежащих ниже вершины зуба на расстоянии hi,
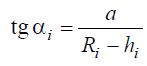
т.е. задний угол по мере приближения точки к центру не уменьшается. Из этого следует, что архимедова спираль отвечает первому требованию, предъявляемому к кривым затылования.
Следует отметить, что при затыловании через каждую из точек режущей кромки, лежащих ниже вершины зуба, проходит эквидистантная архимедова спираль с меньшим шагом Aα. Расчеты показывают, что, например, при переточке фрезы диаметром d = 60 мм с высотой зуба h = 10 мм при повороте передней грани фрезы на 30° от начального положения угол αв на вершине зуба увеличивается от 9° до 9°52′, а у основания зуба — соответственно от 17°39′ до 20°57′. Таким образом, наибольшее влияние на значение угла α оказывает не переточка, а радиус окружности, на которой лежит точка режущей кромки.
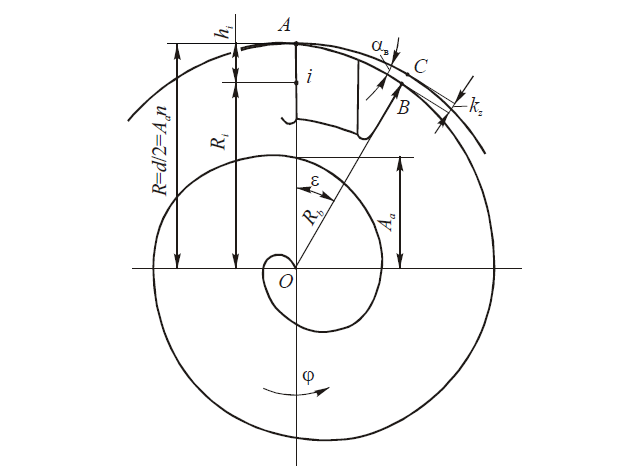
Важным параметром кривой затылования является величина падения затылка kz, которая зависит от величины заднего угла на вершине зуба фрезы αв, диаметра фрезы и числа ее зубьев. Как видно из рис. 1 и рис. 3, величина kz отсчитывается на передней грани соседнего зуба от точки пересечения ее с кривой затылования до вершины зуба, лежащей на наружной окружности. Заштрихованная часть (рис. 1) — это объем металла, удаляемый на вершине зуба при затыловании.
Из рис. 3 следует, что величина падения затылка BC на одном зубе, замеренная на его вершине,
kz = d/2 — RВ = d/2-αφВ
где RВ — радиус-вектор архимедовой спирали в точке B.
При этом d /2 = Aαn, φi = 2πn, если используется участок архимедовой спирали, полученный при n — целом числе оборотов радиуса-вектора или числе шагов спирали (на рис. 3 число шагов n = 2).
Из рис. 3 также следует, что угол поворота радиуса-вектора RB равен
φВ = 2πn — ε
где ε — угловой шаг между зубьями (ε = 2π / z).
Из уравнений выразим значение коэффициента архимедовой спирали для вершины зуба (точка А)
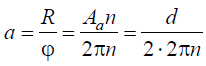
Подставив в уравнение значения α и φВ, получим
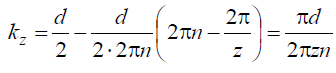
Из уравнения следует, что задний угол вершинной точки зуба tgαВ в точке А может быть найден из соотношения
tgαВ = 1/φА = 1/2πn
Следовательно, величину падения затылка можно выразить как
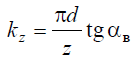
Аналогичное уравнение для определения kz можно также найти из треугольника с криволинейными сторонами АВС, рассматривая его приближенно как прямоугольный треугольник, где АС и ВС — катеты, угол АСВ = 90°. В этом случае AC = πd/ z — окружной шаг зубьев, а катет ВС = kz, αВ — задний угол при вершине треугольника в точке А. Отсюда величина падения затылка равна
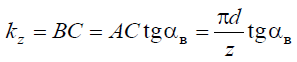
Значение kz указывают на кулачках для затылования. Зная диаметр и число зубьев фрезы и задавшись необходимым значением угла αВ, подбирают нужный кулачок по величине kz, рассчитанной по уравнению. Кулачки для оснащения затыловочных станков изготавливают серийно комплектами с kz = 0,5…12,0 мм (через 0,25 мм для фрез малых диаметров, через 0,5 мм — для фрез средних диаметров и через 1…2 мм — для фрез больших диаметров).
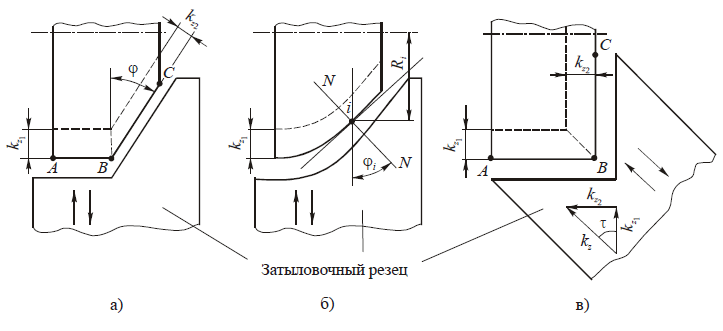
а — на наклонном прямом участке (прямое затылование); б — на криволинейном участке; в — на участке, перпендикулярном оси фрезы (наклонное затылование)
Задние углы на участках режущих кромок, наклонных к оси фрезы.
Приведенные выше формулы для расчета задних углов получены в плоскости, перпендикулярной к оси фрезы, т.е. они справедливы только для участков режущих кромок, параллельных ее оси. Найдем их значения αN в нормальных сечениях на участках, наклонных к оси, в том числе криволинейных. Знать эти углы крайне необходимо, так как от угла αN зависит работоспособность всей фрезы. На рис. 4 показана фреза с ломаной режущей кромкой, часть которой АВ параллельна оси, а участок ВС наклонен. При этом угол наклона φ между нормалью к оси и режущей кромкой может меняться в пределах от 0 до 90°.
Если затыловочный резец совершает возвратно-поступательное перемещение в радиальном направлении (прямое затылование), то на участке АВ величина падения затылка равна
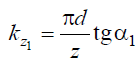
а на участке ВС
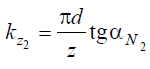
Так как kz2 = kz1 sin φ, то из соотношения этих уравнений следует, что
tg αN2 = tg α1sin φ
С учетом переменного значения радиуса в любой i-й точке наклонного участка режущей кромки
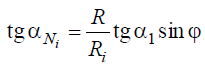
Из уравнения следует, что при φ→0 угол αi уменьшается и на участках режущей кромки, перпендикулярных оси, будет равен нулю. При малых значениях угла φ угол αi должен быть не менее 2…3°, а в исключительных случаях — не менее 1,0…1,5°.
Если наклонные участки имеют криволинейную (выпуклую или вогнутую) форму, то для определения αNi она заменяется касательной (рис. 4, б) и расчет ведется по уравнению с учетом значения угла наклона φ этой касательной.
В случае, когда участок кромки ВС перпендикулярен оси (рис. 4, в), то во избежание нулевых значений угла α применяют наклонное затылование, которое заключается в изменении направления перемещения затыловочного резца от прямого радиального в наклонное к оси фрезы.
Угол поворота суппорта затыловочного станка τ найдем на рис. 4, в, задаваясь необходимыми значениями углов α1 и α2 и, соответственно, величинами kz1 и kz2.
Как видно из рис. 4, в