Затылованные фрезы большей частью изготавливают с передним углом γ = 0°. Это делается с целью упрощения изготовления, переточки и контроля профиля режущих кромок, а также с целью снижения биения зубьев при переточке. В то же время при обработке многих материалов это приводит к увеличению сил резания, снижению стойкости фрез и повышению шероховатости обработанной поверхности. Поэтому при фрезеровании ряда труднообрабатываемых материалов необходимо применять затылованные фрезы с положительным передним углом. Для устранения возможных при этом погрешностей профиля деталей необходимо проводить коррекционные расчеты по определению профиля фрезы и, соответственно, профиля затыловочных резцов в осевом (диаметральном) сечении, в котором производится процесс затылования. Для контроля профиля фрезы с помощью шаблона необходимо также определить профиль фрезы в плоскости передней грани.
Рассмотрим решение этих задач на примере фасонной дисковой фрезы, предназначенной для фрезерования прямой канавки.
Из расчетной схемы (рис. 1) видно, что дно канавки обрабатывается вершинной режущей кромкой, к которой принадлежит точка 1, а боковые стороны канавки — режущими кромками фрезы 1-2′ Точка 2′ фрезы при вращении вокруг оси по окружности радиуса R2 обрабатывает точку 2 заготовки. Проведем через точку 2′ фрезы архимедову спираль, эквидистантно расположенную относительно спирали, которая проходит через точку 1. В осевом (радиальном) сечении О3 найдем высоту зуба фрезы hф2 и перенесем ее в аналогичное сечение О1 путем смещения точки 2′ по архимедовой спирали.
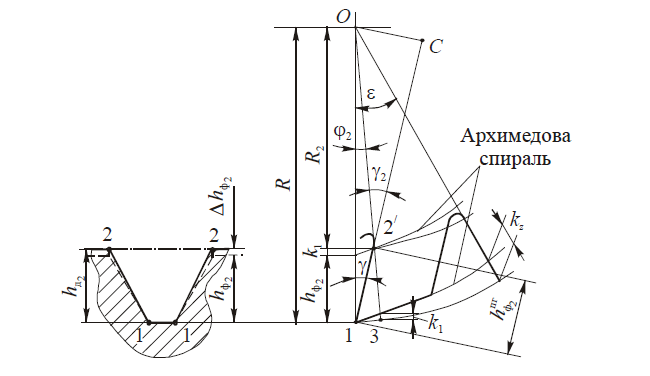
Как видно из рис. 1,
hф2 = hд2 -Δhф2 = hд2 — k1
где h — высота точки 2 профиля детали; k1 — величина падения затылка в точке 3 при повороте радиуса О1 на угол φ2; Δhф2 — величина коррекции профиля фрезы (Δhф2 = k1).
Из рис. 1 следует, что если угол поворота φ будет равен угловому шагу зубьев фрезы φ = ε = 2π/z, то величина падения затылка, отсчитываемая на передней грани соседнего зуба, будет равна
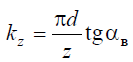
Отсюда можно составить соотношение
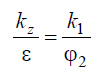
из которого найдем
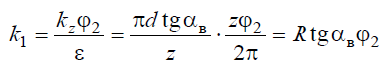
где R — радиус наружной окружности фрезы; αв — задний угол в вершинной точке зуба.
Эти величины заданы в условиях задачи. Необходимо найти угол φ2, выразив его через высоту профиля hд2. Для этого опустим из центра О перпендикуляр OC на продолжение передней грани фрезы и найдем передний угол γ2 в точке 2′, то есть угол между радиусом R2 = R — hд2 и передней гранью. Из треугольника О1С определим, что
OC = Rsin γ = R2 sin γ2
Следовательно,
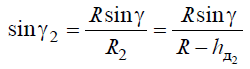
Так как угол γ2 является внешним углом треугольника О12′, то
γ2 =γ + φ2
Следовательно,
φ2 = γ2 — γ
Таким образом, зная по профилю детали значение h, по уравнению найдем значение угла γ2 и значение угла φ2. Затем найдем величину коррекции профиля Δhф2 = k1 . Отложив ее по высоте от hд2 , можно построить профиль фрезы в осевом сечении, соединив точку 2 фрезы с точкой 1. При этом учитывают, что размеры профиля вдоль оси у детали и фрезы совпадают.
Размеры профиля фрезы вдоль передней грани получим из треугольника О1С:
hпгф2 = R cos γ — R2cos γ2 = R(cos γ — cos γ2) + hд2cos γ2
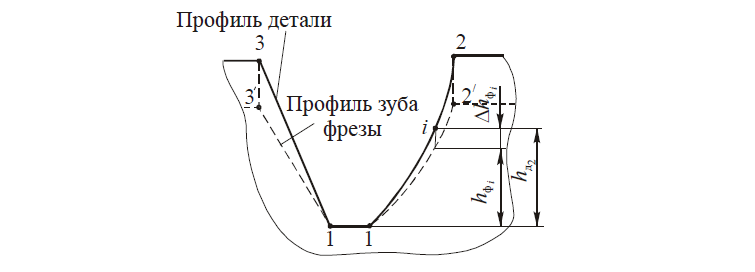
Если стенки канавок криволинейны (рис. 2), то для построения профиля требуется найти высотные координаты нескольких промежуточных точек. Для любой i-й точки можно воспользоваться уравнениями, сменив в них индекс 2 на индекс i. При этом кривая профиля фрезы будет отличаться от кривой профиля изделия. Для упрощения ее можно аппроксимировать более технологичной кривой. например дугой окружности в пределах допуска на погрешность профиля.
Значения передних и задних углов, принятые при расчете таких фрез, обычно задаются в следующих пределах: γ = 10…20°, αв = 8…10°.
