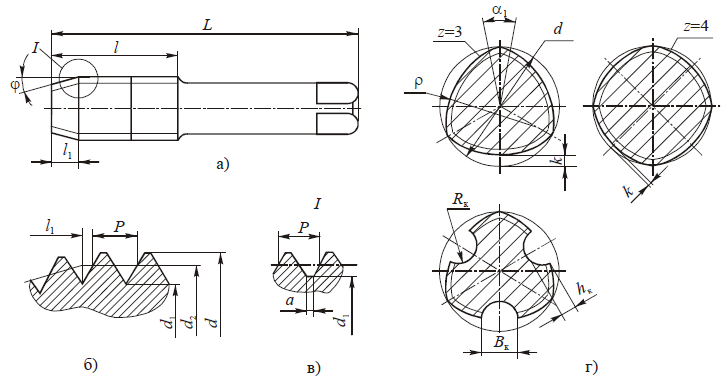
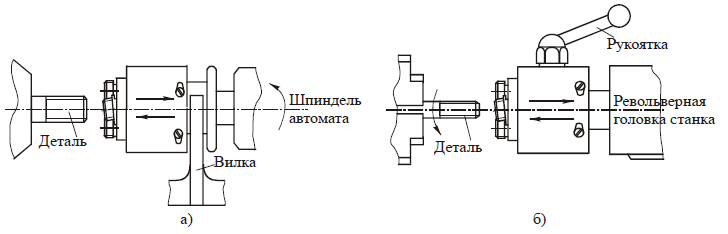
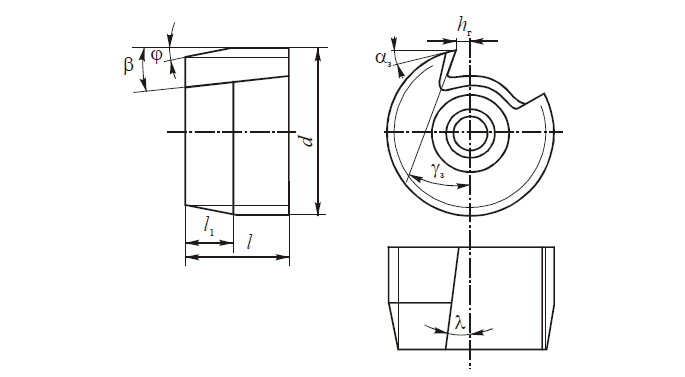
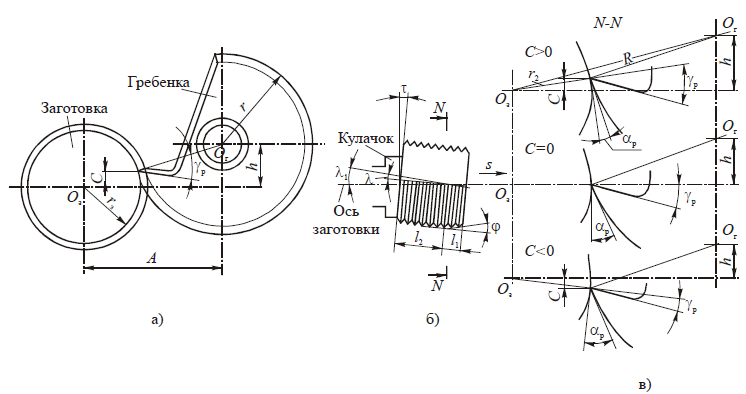
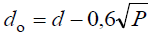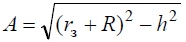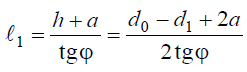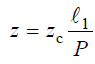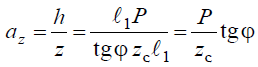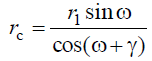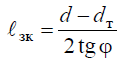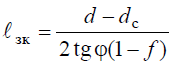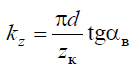Уравнение эвольвенты.
Профиль боковых сторон зубьев зубчатых колес с эвольвентным зацеплением представляет собой две симметрично расположенные эвольвенты.
Эвольвента — это плоская кривая с переменным радиусом кривизны, образованная некоторой точкой на прямой, обкатывающейся без скольжения по окружности, диаметром (радиусом) db(rb), называемой основной окружностью.
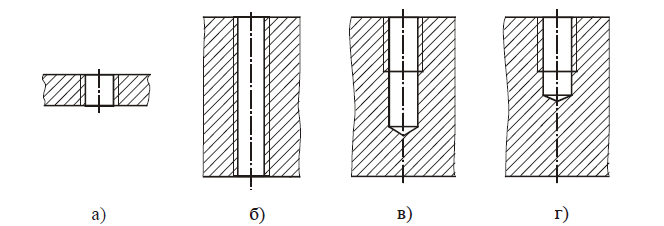
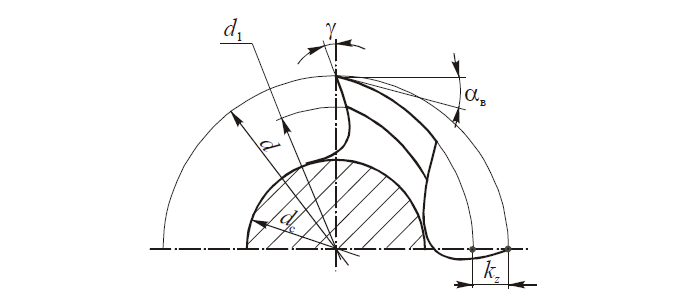
На рис. 1, а показано построение эвольвенты, а на рис. 1, б — расчетная схема для определения координат точки М, находящейся на прямой ВМ. Из условия обката без скольжения ВМ = АВ.
Здесь ВМ — нормаль к эвольвенте и одновременно радиус ρм кривизны эвольвенты в точке М; θм — угол, отсчитываемый от начала эвольвенты до точки М; vм — угол развернутости эвольвенты; αм — угол профиля эвольвенты в точке М (угол между касательной к эвольвенте и радиусом rм).
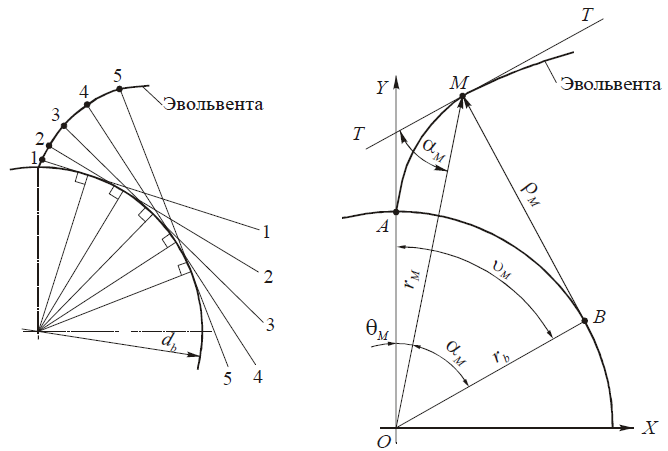
а — построение эвольвенты; б — расчетная схема
Так как ВМ = АВ, то rb ∙ tgαм = rb.vM. Следовательно, vм = tgαм, θм = vм — αм и θм=tgαм—αм = invαм.
Угол θм = invαм называется инволютой или эвольвентным углом. В справочниках имеются специальные таблицы инволют: invαм = f (αм ).
Уравнение эвольвенты в полярных координатах на основании рис. 1 выглядит так:
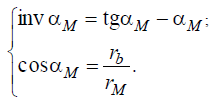
Чтобы построить эвольвенту, нужно задать значение радиуса rм некоторой точки М и при определенном радиусе основной окружности rb найти значение cos αм, а затем по углу αм найти эвольвентный угол θм = inv αм.
Уравнение эвольвенты можно записать также в декартовых координатах X-Y. Из ΔОВМ следует, что
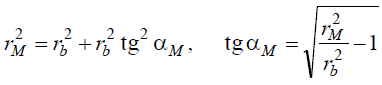
Координаты точки М, т.е. уравнение эвольвенты:
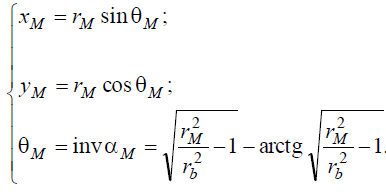
Радиус основной окружности rb найдем для точки, лежащей на делительной окружности радиуса r = mz / 2 , в которой угол профиля стандартного эвольвентного зацепления α = 20°. Тогда из уравнения найдем, что
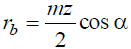
Характерной особенностью эвольвенты является переменность угла профиля αм и радиуса кривизны ρм в каждой из ее точек.
Из рис.1, б следует, что
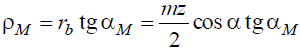
При z → ∞ ρм → ∞, то есть эвольвента превращается в прямую линию, которую можно рассматривать как частный случай эвольвенты. Отсюда следует, что характер эвольвентного зацепления не изменится, если колесо будет сцепляться с рейкой, имеющей z = ∞ и прямолинейный профиль зубьев с углом α=20°, то есть становится возможным нарезание эвольвентных колес инструментами реечного типа (гребенки, червячные фрезы) методом обкаточного огибания.
Основные параметры эвольвентного зацепления.
На рис. 2 показано зацепление двух зубчатых колес с эвольвентным профилем. Рассмотрим основные параметры зацепления, их определения и стандартные обозначения.
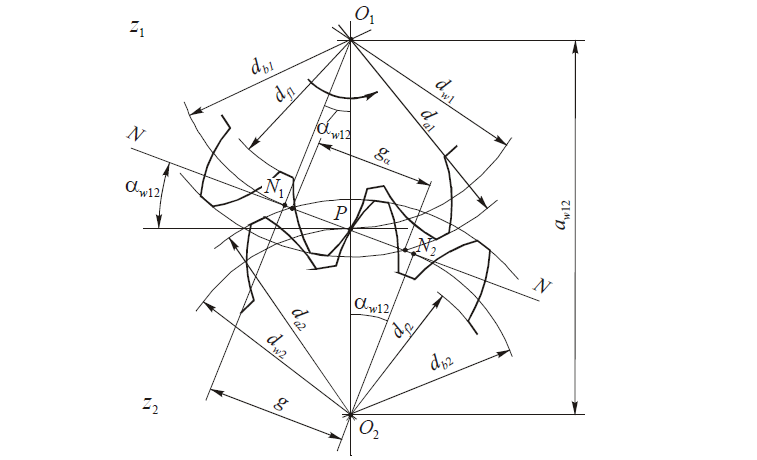
В отличие от принятого ранее, обозначение всех параметров производится строчными, а не заглавными буквами с индексами, указывающими их принадлежность колесу, инструменту, типу окружности и виду сечения.
Стандартом предусмотрены три группы индексов:
• первая группа: п, t, x — означает вид сечения, соответственно, нормальный, торцевой (окружной), осевой;
• вторая группа: a, f, b, w, y — означает, что параметр относится соответственно к окружностям выступов, впадин, основной, начальной и любой концентричной окружности. Для делительной окружности индекс не указывается;
• третья группа индексов: 1, 2, 0 — означает, что параметр относится соответственно к шестерне, колесу, зуборезному инструменту.
Порядок использования индексов определяется номером группы, т.е. вначале предпочтение отдается индексам первой группы, затем второй и т.д.
Некоторые индексы разрешается опускать в случаях, исключающих возникновение недоразумений или не имеющих применения по определению. Например, у прямозубых цилиндрических колес не используются индексы первой группы. В ряде случаев некоторые индексы с целью сокращения записи также опускаются.
Рассмотрим зацепление двух прямозубых цилиндрических (рис. 2) колес: с меньшим числом зубьев (z1), называемого шестерней, и с большим числом зубьев (z2), называемого колесом; соответственно с центрами колес в точках О1 и О2. В процессе обката шестерни с колесом происходит качение без скольжения двух центроид — окружностей, соприкасающихся в полюсе зацепления — Р. Эти окружности называются начальными, а их диаметры (радиусы) обозначаются с индексом w: dw1 (rw1), dw2 (rw2). Для некорригированных колес эти окружности совпадают с делительными окружностями, обозначение диаметров (радиусов) которых дается без индексов первой и второй групп, т.е. для шестерни — d1(r1), для колеса — d2(r2).
Делительная окружность — окружность, на которой шаг между зубьями и угол профиля равны им же на делительной прямой зубчатой рейки, сцепленной с колесом. При этом шаг P = πm — расстояние между двумя соседними одноименными сторонами профиля. Отсюда диаметр делительной окружности колеса равен
d = Pz / π = mz
Модуль зуба m = P/ π — величина условная, имеющая размерность в миллиметрах (мм) и используемая как масштаб для выражения многих параметров зубчатых колес. В зарубежной практике в этом качестве используется питч — величина обратная модулю.
Основная окружность — это окружность, от которой образуется эвольвента. Все параметры, относящиеся к ней, обозначаются с индексом b, например, диаметры (радиусы) колес в зацеплении: db1 (rb1), db2 (rb).
Касательно к основным окружностям через полюс зацепления Р проходит прямая N—N, а ее участок N1—N2 называется линией зацепления. По ней в процессе обката перемещается точка контакта сопрягаемых профилей колес. N1—N2 называется номинальной (теоретической) линией зацепления, обозначаемой буквой g. Расстояние между точками пересечения ее с окружностями выступов колес называется рабочим участком линии зацепления и обозначается ga.
В процессе обката зубчатых колес точка контакта профилей перемещается в пределах активного (рабочего) участка линии зацепления ga, которая является нормалью к профилям обоих колес в этих точках и одновременно общей касательной к обеим основным окружностям.
Угол между линией зацепления и перпендикуляром к линии, соединяющей центры сопрягаемых колес, называется углом зацепления. У корригированных колес этот угол обозначается αw12, для некорригированных колес αw12 = α0.
Межцентровое расстояние некорригированных колес
αw12 = rw1 + rw2 = r1 + r2 = m(z1 + z2)/2.
Окружности выступов и впадин — окружности, проходящие соответственно через вершины и впадины зубьев колес. Их диаметры (радиусы) обозначаются: da1(ra1), df1(rf1), da2(ra2), df2(rf2).
Шаги зубьев колес — Pt, Pb, Pn, Px — это расстояния между одноименными сторонами профиля, замеренные:
а) по дуге делительной окружности в торцевом сечении — окружной (торцевый) шаг Pt = πd / z;
б) по дуге основной окружности — основной шаг Pb = πdb / z;
в) по контактной нормали (линии зацепления) — основной нормальный шаг Pbn;
г) по нормали к направлению зубьев и по оси (у винтовых передач) — нормальный шаг Pn и осевой шаг Px.
Коэффициент перекрытия ε — отношение активной (рабочей) части линии зацепления к основному нормальному шагу:
ε = ga /Pbn
Окружная (торцевая) толщина зуба St — длина дуги делительной окружности, заключенная между двумя сторонами зуба. Толщина, измеренная по хорде, обозначается как S.
Окружная ширина впадины между зубьями e — расстояние между разноименными сторонами профиля по дуге делительной окружности.
Высота головки зуба ha — расстояние между окружностями выступов и делительной: ha = ra — r.
Высота ножки зуба hf — расстояние между окружностями делительной и впадин: hf = r — rf.
Высота зуба: h = ha + hf.
Рабочий участок профиля зуба — геометрическое место точек контакта профилей сопрягаемых колес, определяется как расстояние от вершины зуба до точки начала эвольвенты. Ниже последней следует переходная кривая.
Переходная кривая профиля зуба — часть профиля от начала эвольвенты, т.е. от основной окружности до окружности впадин. При методе копирования соответствует форме головки зуба инструмента, а при методе обкатки образуется вершинной кромкой режущего инструмента и имеет форму удлиненной эвольвенты (для инструментов реечного типа) или эпициклоиды (для инструментов типа колеса).
Другие параметры и обозначения будут приведены ниже по мере использования.
Понятие об исходном контуре рейки.
Как было показано выше, частным случаем эвольвенты при z = ∞ является прямая линия.
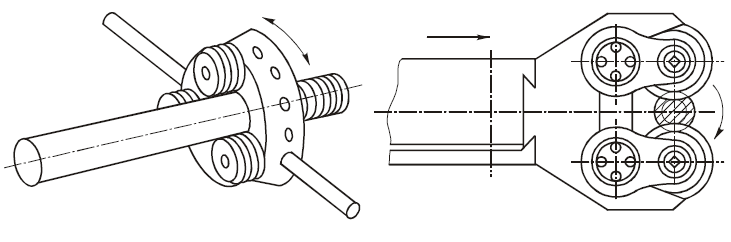
Это дает основание использовать в эвольвентном зацеплении рейку с прямобочными зубьями. При этом любое зубчатое колесо данного модуля независимо от числа зубьев может быть сцеплено с рейкой того же модуля. Отсюда возникла идея обработки колес методом обкатки. В зацеплении колеса с рейкой (рис. 3) радиус начальной окружности последней равен бесконечности, а сама окружность превращается в начальную прямую рейки. Линия зацепления N1N2 проходит через полюс P касательно к основной окружности колеса и перпендикулярно к боковой стороне профиля зуба рейки. В процессе зацепления начальная окружность колеса обкатывается по начальной прямой рейки, а угол зацепления становится равным углу профиля зуба рейки α.
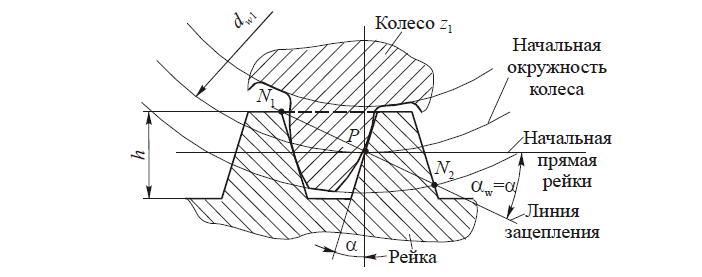
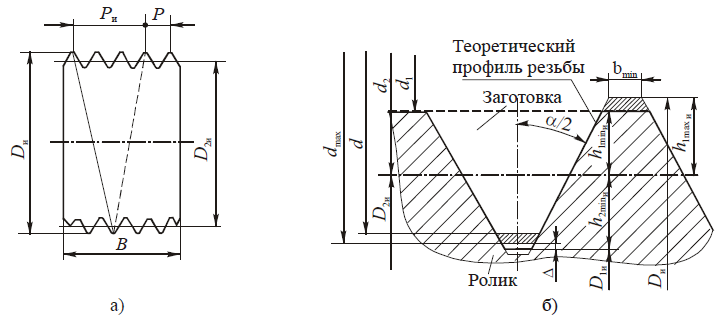
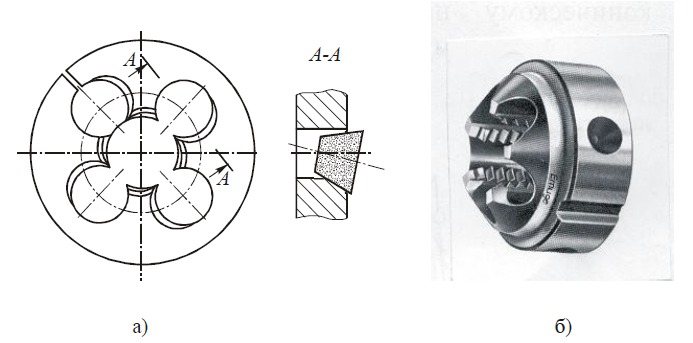
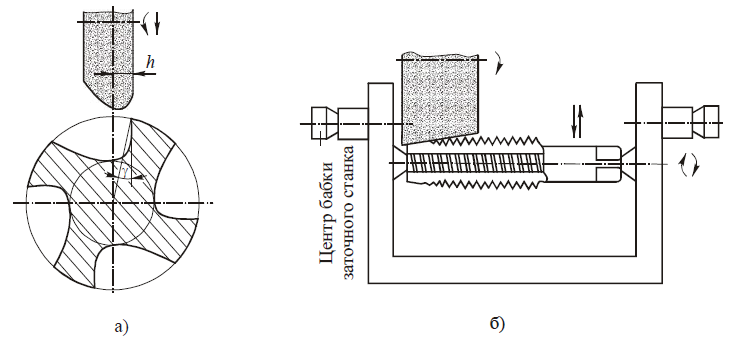
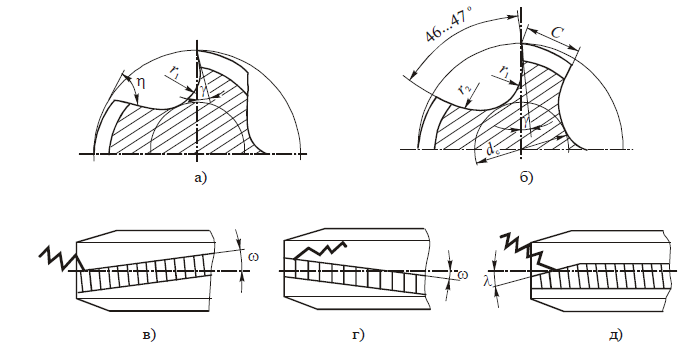
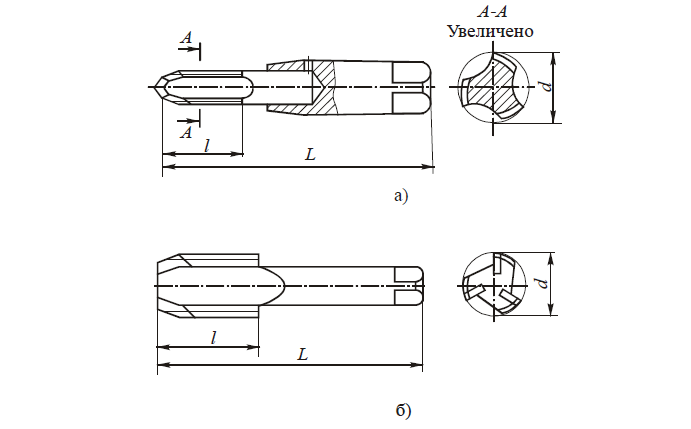
Так как профиль зубьев рейки — прямая линия, это в значительной мере упрощает контроль линейных параметров зубьев и угла профиля. С этой целью стандартами установлено понятие исходного контура зубчатой рейки (рис. 4, а).
В соответствии со стандартами, принятыми в нашей стране для эвольвентного зацепления, исходный контур имеет следующие параметры зубьев в зависимости от модуля:
- угол профиля α = 20°;
- коэффициент высоты головки hα* = 1;
- коэффициент высоты ножки hf* = 1,25;
- коэффициент радиального зазора с* = 0,25 или 0,3;
- коэффициент граничной (рабочей) высоты зуба hL* = 2;
- шаг зубьев P = πт;
- толщина зуба S и ширина впадины е: S = e = 0,5P = πт / 2.
Делительная прямая рейки проходит по середине рабочей высоты зуба hL.
Для зуборезных инструментов основные параметры зубьев по аналогии с изложенным выше задаются параметрами исходной инструментальной рейки (рис. 4, б). Так как зубья режущего инструмента обрабатывают впадину между зубьями колеса и могут нарезать колеса с модифицированным (фланкированным) профилем, между названными исходными контурами имеются существенные различия, а именно:
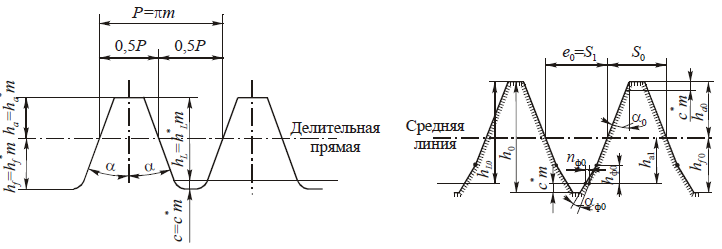
а — зубчатой рейки; б — инструментальной рейки
- Высота головки зуба исходной инструментальной рейки ha0 = (hf0* + c0*)m = 1,25m, т.е. коэффициент высоты головки hα0* = 1,25. Высота ножки зуба hf0 = 1,25т , а полная высота зуба h0 =ha0 +hf0 = 2,5m.
- Если нарезаемое колесо имеет срез у головки (модифицированный профиль), то ножка зуба инструментальной рейки должна иметь утолщение с параметрами hф0, αф0, nф0.
3. Толщина зуба у зубчатой рейки S = πт /2, а у инструментальной рейки при нарезании колес с модифицированным профилем зубьев
S0 = πт/2 ± ΔS0
Поправка ΔS0 берется из справочников в зависимости от величины модуля зуба. Знак «+» берется для чистовых, а знак «-» — для черновых инструментов. В первом случае происходит утонение зубьев нарезаемого колеса с целью создания бокового зазора между зубьями сцепляемых колес, во втором случае утолщение, в результате чего нарезаемые зубья получают припуск на чистовую обработку.
У колес с обычным (немодифицированным) профилем зубьев изменение толщины нарезаемых зубьев можно получить путем смещения инструментальной рейки относительно центра колеса и утолщение ее зубьев у ножки не требуется.
Параметры зацепления корригированных зубчатых колес.
Корригирование (исправление) колес дает возможность улучшить зубчатое зацепление по сравнению с нормальным зацеплением в отношении трения, износа и прочности зубьев, уменьшить вероятность подреза ножки зубьев при малом их числе и др.
Применительно к долбякам корригирование дает возможность получения задних углов на режущих кромках (см. ниже).
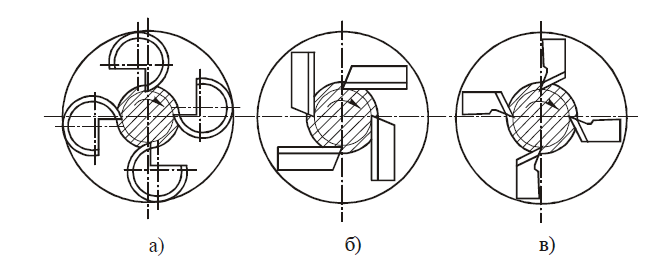
Из известных методов корригирования на практике наибольшее применение нашло высотное корригирование, которое осуществляется путем смещения профиля исходной инструментальной рейки относительно центра нарезаемого колеса. Такое смещение принято считать положительным, если рейка отводится от центра колеса, и отрицательным, когда она приближается к его центру (рис. 5). Величина смещения оценивается произведением x0∙m, где х0 — коэффициент смещения.
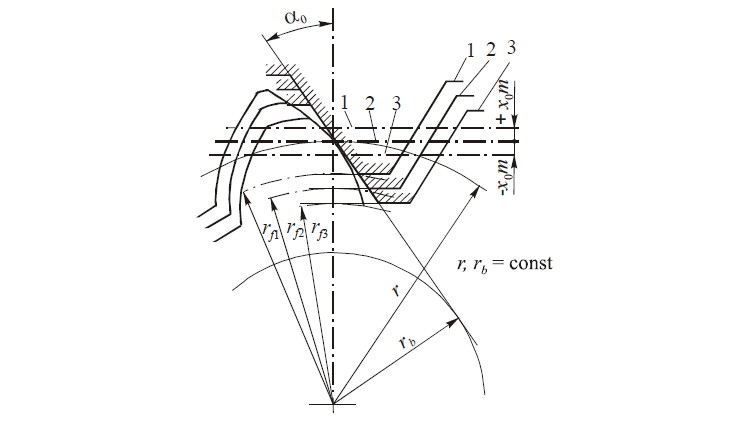
1 — положительное смещение; 2 — нулевое смещение; 3 — отрицательное смещение
При положительном смещении высота головки зуба нарезаемого колеса h’a1 увеличивается на величину x0∙m, а высота ножки h’f1 уменьшается на ту же величину. При отрицательном смещении, наоборот, высота головки зуба уменьшается, а высота ножки увеличивается. Полная высота зуба колеса в обоих случаях остается неизменной, при этом положение делительной и основной окружностей колеса постоянно и не зависит от величины смещения, то неизбежно изменение толщины зуба нарезаемого колеса по делительной окружности из-за смещения делительной прямой рейки относительно начального положения на величину ±x0m. Как видно из рис. 6, толщина зуба по делительной окружности у корригированного колеса при смещении рейки инструмента
S’1,3= πm/2 ± 2ΔS = πт/2 ± 2x0mtgα0
где ΔS = x0m tgα0 .
Знак «+» берется при положительном, а знак «-» — при отрицательном смещении.
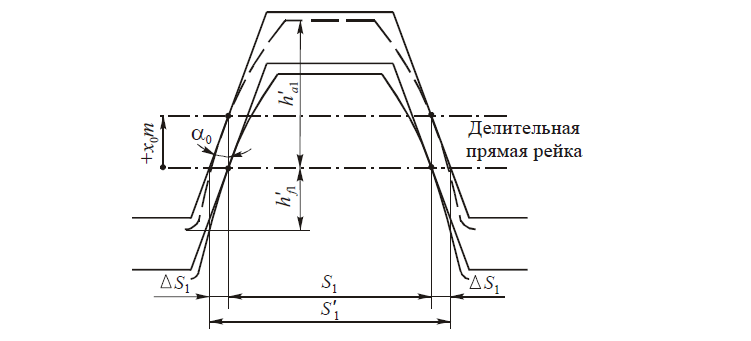
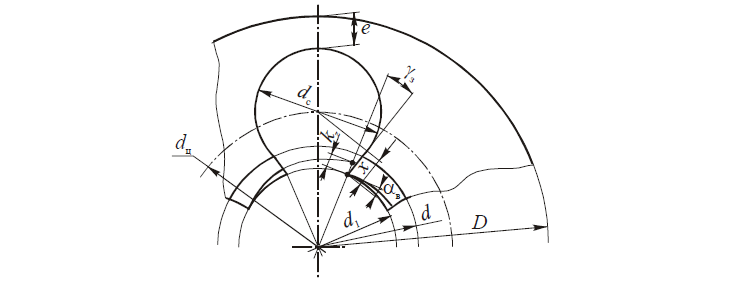
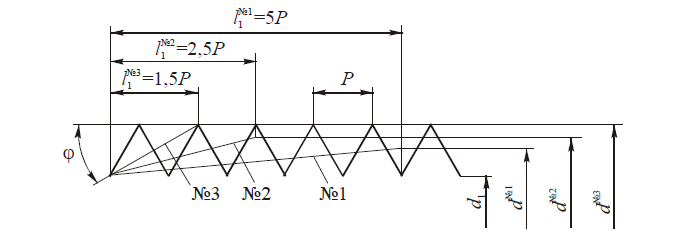
При расчетах зуборезных инструментов, например долбяков, зубья которых корригированы, возникает необходимость определения толщины зуба на окружности любого радиуса — rу, концентричной с делительной окружностью радиусом r.
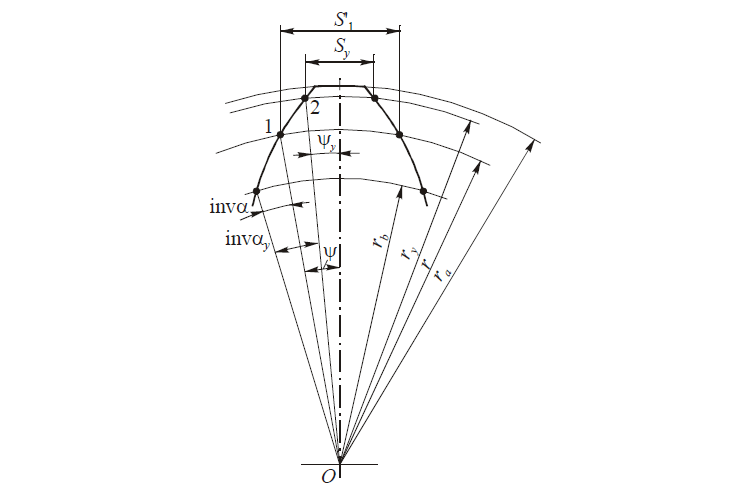
Из рис. 7 и уравнения эвольвенты следует, что толщина зуба по окружности радиуса ry в точке 2 равна
Sy = 2rу∙ψу
где ψу = ψ — (invαy — invα); ψ и ψу — углы между линией симметрии зуба и радиусами, проведенными в точке 1 на делительной окружности и в точке 2 на окружности радиусом ry; invα и invαy — эвольвентные углы в этих точках.
Так как толщина зуба на делительной окружности S‘1 — величина известная, а угол ψ = S‘1 /2r , то Sy можно определить по формулам:
для корригированных колес
Sy = 2ry(S‘1/2r + inv α — inv αy)
для некорригированных колес при S = πm / 2
Sy = dy (πm / 2d + inv α — inv αy )
Здесь углы α и αy, как следует из уравнения, определяются по следующим формулам: cosα = rb /r, cosαу = rb /rу.
На рис. 8 представлено зацепление двух колес с корригированными зубьями. Его главная особенность заключается в том, что начальные окружности rw1 и rw2, проходящие через полюс зацепления Р, не совпадают с делительными окружностями r1 и r2. По этой причине угол зацепления αw12 колес не равен углу профиля исходной рейки, толщины зубьев на делительной окружности меняются, а также меняются соотношение высот головок и ножек зубьев, диаметры окружностей выступов, впадин и межцентровое расстояние между колесами.
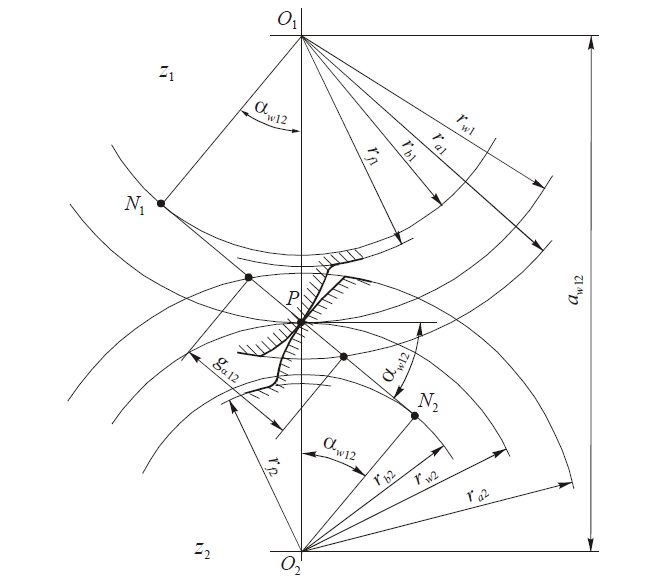
Угол зацепления aw12 — это угол между линией зацепления N1N2 и перпендикуляром к прямой, соединяющей центры колес (для корригированных колес αw12≠α).
Формулу для расчета αw12, а точнее inv αw12, найдем в следующей последовательности:
1. Запишем уравнение для расчета толщин зубьев на начальной окружности Sw1 и Sw2 для шестерни и колеса на основании формулы, сменив индекс y на w.
2. Сумма толщин зубьев колес, находящихся в зацеплении, равна шагу на начальной окружности:
Sw1+Sw2 = Pw12
Путем алгебраических преобразований найдем эвольвентный угол inv αw12.
Толщины зубьев на начальных окружностях шестерни и колеса на основании уравнения
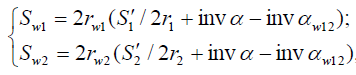
где r1, r2 — радиусы делительных окружностей (r1 = mz1 /2; r2 = mz2 /2);
S‘1, S’2 — толщины зубьев по делительным окружностям.
Шаг зубьев на начальных окружностях шестерни и колеса будет один и тот же:
Pw12 = 2πrwl / z1 = 2πrw2 / z2
Из уравнения следует, что
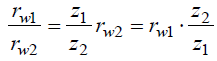
Подставим параметры:
2πrw1 / z1 = 2rw1(S‘1 / 2r1 + inv α — inv αw12) + 2rw12z2 / z1 (S’2/2r2 + inv α- inv αw12)
Сократим обе стороны равенства на 2rw1 и умножим на z1. В итоге получим
π = S‘1 / m + z1 inv α — z1 inv αw12 + S’2 / m + z2 inv α — z2 inv αw12
После преобразования
(z1 + z2)inv αw12 = (z1 + z2)inv α + S‘1 /m + S’2m — π
Отсюда
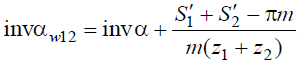
Из этого уравнения следует, что если колесо z1 находится в зацеплении с инструментами реечного типа (червячная фреза, гребенка), у которых z2 = ∞, то второй член правой части уравнения превращается в нуль и угол зацепления передачи становится равным углу профиля исходного контура рейки, т.е. αw12 = α0.
Для инструментов типа колеса (долбяк, шевер) уравнение желательно представить в виде зависимости inv αw10 от величины смещения профиля пары корригированных колес z1 и z0. Для этого подставим значения S1 и S2, рассчитанные по формуле:
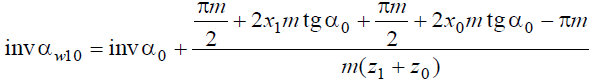
или после сокращений
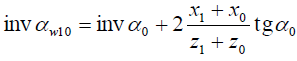
где α0 — угол профиля инструмента.
Межцентровое расстояние у корригированных колес
αw12 = rw1 + rw2
Так как радиусы начальных окружностей равны
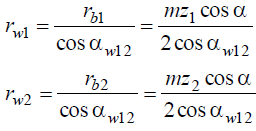
тогда
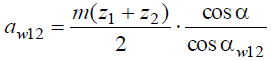
Номинальная длина линии зацепления (рис. 8):
g = N1P+ N2P = rw1 sin αw12 + rw2 sin αw12 = αw12 sin αw12
Длина активной части линии зацепления сопряженных колес равна расстоянию между точками пересечения линии зацепления окружностями выступов шестерни и колеса (рис. 8):
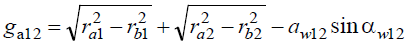
Радиусы окружностей выступов и впадин у корригированного колеса с учетом смещения ±x0m:
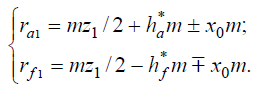
При этом высота зуба колеса h = hα = hƒ от величины смещения профиля не зависит. Из-за разности знака у головки и ножки, т.е.
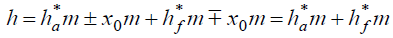
здесь и выше верхний знак используется при положительном смещении, а нижний — при отрицательном смещении профиля.
Возможен частный случай, когда пара «шестерня — колесо» или «колесо — инструмент» имеет одинаковые по величине, но обратные по знаку величины смещения (так называемое нулевое зацепление), тогда делительные окружности совпадают с начальными. Как следует из уравнения, в этом случае угол зацепления αw12 = α, но меняются толщина зубьев по делительной окружности и соотношение высот головок и ножек зубьев. В этом случае межцентровое расстояние равно
αw12 = (d1 +d2)/2 = m(z1 + z2)/2.
Такая коррекция применяется при больших передаточных числах. При ней обычно положительное смещение берется для шестерни с целью увеличения прочности зубьев, т.е. имеет место только высотная коррекция.
При угловой коррекции шестерню и колесо изготавливают обычно с положительным смещением исходного контура. Угол зацепления у таких колес будет больше, чем у некорригированных (отсюда и название — «угловая коррекция»). Основное преимущество угловой коррекции перед высотной состоит в том, что она дает возможность увеличить прочность зубьев как у шестерни, так и у колеса.
Если величина или знаки коррекции у нарезаемых колес не совпадают, то имеет место совмещение угловой и высотной коррекции одновременно.